Математическая статистика в горно-геологических расчетах, страница 19

 Имеем параметры выборок

 по признаку Х:  n₁ – объем выборки;  – выборочная средняя; S_x² – исправленная выборочная дисперсия;

 по признаку У:  n₂ – объем выборки; – выборочная средняя; S_у² – исправленная выборочная дисперсия.

Требуется при заданном уровне значимости a сравнить  математические ожидания М(Х) и М(У) генеральных совокупностей.

Перед тем, как решать поставленную задачу, нужно убедиться, что дисперсии сравниваемых совокупностей равны (см. п. 4.1). Далее решение осуществляется следующим образом: выдвигается основная и альтернативная гипотезы.  Рассмотрим три случая:

а)  Н₀: M(Х) = M(У)     б)  Н₀: M(Х) = M(У)      в)  Н₀: M(Х) = M(У)         

     Н₁: M(Х) > M(У)          Н₁: M(Х) < M(У)            Н₁: M(Х) ¹ M(У)

Для проверки гипотез по результатам выборок вычисляем наблюдаемое значение критерия                 

            .   

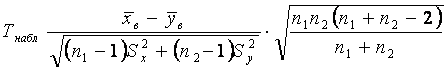Этот критерий является случайной величиной, которая подчиняется закону распределения Стьюдента с  k = n₁ + n₂ – 2 степенями свободы.

Критические области и точки зависят от выдвинутых альтернативных гипотез  H₁ .

а)     Н₁: M(Х) > M(У)

Критическая область является правосторонней. Критическая точка находится по таблице критических точек распределения Стьюдента (приложение 6, односторонняя критическая область)  

               t_кр = t(a ; k),  где a – заданный уровень значимости.

Если в результате сравнения окажется ôT_наблô < t_кр, то нет оснований отвергнуть нулевую гипотезу H₀; если же  ôT_наблô >  t_кр , то нулевая гипотеза H₀ отвергается; принимается гипотеза H₁.

б)  Н₁: M(Х) < M(У)

Критическая область является левосторонней. Критическая точка находится по таблице критических точек распределения Стьюдента (приложение 6, односторонняя критическая область), только с отрицательным знаком

               t_кр = – t(a; k),  где a – заданный уровень значимости.

Если в результате сравнения окажется ôT_наблô< t_кр, то нет оснований отвергнуть нулевую гипотезу H₀; если же  ôT_наблô>  t_кр , то нулевая гипотеза H₀ отвергается; принимается гипотеза H₁.

в)       Н₁: M(Х) ¹ M(У)

Критическая область является двусторонней. Критическая точка находится по таблице критических точек распределения Стьюдента (приложение 6, двусторонняя критическая область) 

                 t_кр = t(a; k),  где a – заданный уровень значимости.

Если в результате сравнения окажется ôT_наблô< t_кр, то нет оснований отвергнуть нулевую гипотезу H₀; если же  ôT_набл ô>  t_кр , то нулевая гипотеза H₀ отвергается; принимается гипотеза H₁.

4.3 Сравнение двух вероятностей биномиальных распределений

Пусть в двух генеральных совокупностях (С1 и С2) производятся независимые испытания. В результате каждого испытания событие А может появиться в первой совокупности с неизвестной вероятностью р₁, во второй –  с неизвестной вероятностью р₂.

Имеем параметры выборок

 по С1:  n₁ – количество испытаний; m₁ – частота появления события А в этих испытаниях, w₁ = m₁/ n₁ – относительная частота (выборочная доля) события А в совокупности С1.