Математическая статистика в горно-геологических расчетах, страница 25

После заполнения 8–го столбца отмечаем, что два последних элемента в этом столбце меньше пяти. Поскольку в   критерии Пирсона требуется, чтобы в каждом интервале было не меньше пяти единиц, то объединим частоты трех последних интервалов N_i^*  – для  8–го столбца;   N_i – для  3–го столбца.

11–ый столбец заполняем по формуле:  В_i =  .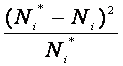

12–ый столбец – контрольный. Он вычисляется по формуле:

    V_i =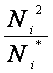 

Сделаем проверку: 50 + 1,5034 = 51, 5034.    Верно.

Заметим, что в результате проверки значения правой и левой частей могут отличатся незначительным образом.

          Запишем наблюдаемое значение критерия:  c²_набл = 1,5034.

Выберем уровень значимости ошибки  a=0,05.

Число степеней свободы равно k=m –2 – 1 , где  m  – число интервалов после объединения. В нашем случае число интервалов после объединения m= 5.   Тогда число степеней свободы равно   k=5–3 = 2.  По таблице критических точек c²  (Приложение 5) находим     c²_кр(0,05; 2)=6.

Сравниваем:        c²_набл < c²_кр .

Следовательно, нет оснований отвергнуть гипотезу о нормальном законе распределения признака Y . Поэтому принимается гипотеза о нормальном распределении признака У.

Пример 3. В результате опыта получены данные по времени безотказной работы стопора путевого ( в часах).