Г). По результатам выборки вычисляют наблюдаемое значение критерия и определяют область, в которую полученное значение критерия попадает. Если наблюдаемое значение критерия попало в критическую область, то гипотезу Н0 отвергают и принимают гипотезу Н1. Если наблюдаемое значение критерия попало в допустимую область, то говорят, что нет оснований отвергнуть гипотезу Н0 .
В математической статистике изучено множество различных гипотез, каждая из которых проверяется своим способом. Рассмотрим некоторые из них, наиболее часто встречаемых в горно-геологических статистических расчетах.
Имеем параметры выборок
по признаку Х: n1 – объем выборки; Sx2 – исправленная выборочная дисперсия;
по признаку У: n2 – объем выборки; Sу2 – исправленная выборочная дисперсия.
Пусть для определенности Sx2 > Sу2.
Требуется при заданном уровне значимости a сравнить дисперсии D(X) и D(Y) генеральных совокупностей.
Выдвинем основную и альтернативную гипотезы. Здесь рассмотрим два случая:
а) Н0: D(Х) = D(У) б) Н0: D(Х) = D(У)
Н1: D(Х) > D(У) Н1: D(Х) ¹ D(У)
Для проверки гипотез по результатам выборок вычисляем наблюдаемое значение критерия (отношение большей дисперсии к меньшей):
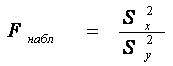
Этот критерий является случайной величиной, которая подчиняется закону распределения Фишера–Снедекора.
Критические области и точки зависят от выдвинутых альтернативных гипотез H1 .
а) Н1: D(Х) > D(У)
Критическая область является правосторонней. Критическая точка находится по таблице критических точек распределения Фишера–Снедекора (приложение 7)
Fкр=F(a; k1; k2),
где a – заданный уровень значимости; k1 = n1 –1 - число степеней свободы большей исправленной дисперсии (Sx2); k2 = n2 –1 - число степеней свободы меньшей исправленной дисперсии (Sy2).
Если в результате сравнения окажется Fнабл < Fкр, то нет оснований отвергнуть нулевую гипотезу H0; если же Fнабл > Fкр , то нулевая гипотеза H0 отвергается; принимается гипотеза H1.
б) Н1: D(Х) ¹ D(У)
Критическая область является двусторонней. Критическая точка находится по таблице критических точек распределения Фишера–Снедекора (приложение 7)
Fкр=F(a/2; k1; k2),
где a – заданный уровень значимости; k1 = n1 –1 - число степеней свободы большей исправленной дисперсии (Sx2); k2 = n2 –1 - число степеней свободы меньшей исправленной дисперсии (Sy2).
Если в результате сравнения окажется Fнабл < Fкр, то нет оснований отвергнуть нулевую гипотезу H0; если же Fнабл > Fкр , то нулевая гипотеза H0 отвергается; принимается гипотеза H1.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.