Математическая статистика в горно-геологических расчетах, страница 15

ån_i(u_i+1)² = 117;  ån_iu_i² = 141; ån_iu_i = –37,   n = 50

     117 = 141 + 2·(–37) + 50  –  верно.

Из таблицы находим условные моменты:

М₁ =  -37/50 = –0,74;   М₂ = 141/50 = 2,82.

Выборочная средняя равна:

 =М₁·h +C =  –0,74×1,48+8,38= 7,2848.

Выборочная дисперсия равна:

D_в = [M₂  - (M₁)²]·h²  =  [2,82 – (-0,74²]·1,48²  = 4,97746.

Выборочное среднее квадратическое отклонение равно

 2,23102 .

S ² =  5,07905 ;

 2,25367 .

Обозначим результат  S _у = 2,25367 .

Полученные результаты позволяют сделать следующие выводы.

Средняя производительность труда рабочего очистного забоя для струговых установок на антрацитовых шахтах  по выборке равна 7,28 тонны за выход. Средний разброс производительности труда рабочего очистного забоя для струговых установок на антрацитовых шахтах  вокруг среднего по выборке равен 2,25 тонны за выход.

3 Интервальные оценки параметров распределения

          Интервальной называют оценку, которая задается интервалом, покрывающим оцениваемый параметр генеральной совокупности. Доверительным называется интервал (a,b), который с заданной вероятностью g покрывает оцениваемый параметр генеральной совокупности. Вероятность g попадания оцениваемого параметра в доверительный интервал (a,b) называется доверительной вероятностью.

3.1    Доверительные интервалы для некоторых параметров распределения

Доверительный интервал для оценки математического ожидания a нормально распределенного количественного признака Х при известном среднем квадратическом отклонении s генеральной совокупности задается формулой:

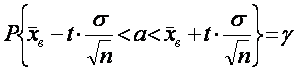 ,                                           (1)

где g = 2Ф(t) – доверительная вероятность;   – точность оценки.

Данная формула применяется для оценки математического ожидания М(Х) = а в двух случаях:

v если известно СКО – s(х)=s;

v если СКО неизвестно, но объем выборки достаточно велик (n > 30). В этом случае в качестве s берут ее оценку S.

Доверительный интервал для оценки математического ожидания a нормально распределенного количественного признака Х при известном среднем квадратическом отклонении s генеральной совокупности задается формулой:

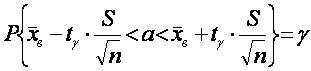 ,                                        (2)

где t_g = t(g,n)  –находят по таблице приложения 3;   – точность оценки.

Доверительный интервал для оценки среднего квадратического отклонения s нормально распределенного количественного признака Х задается формулой:

P{S(1 – q) < s <S(1+q)} = g ,   при q < 1                      (3)

P{0 < s <S(1+q)} = g ,            при q > 1  .                     (4)

Здесь исправленное выборочное среднее квадратическое отклонение S служит оценкой для генерального  среднего квадратического отклонения s ;

q=q(g,n) – находят по таблице приложения 4;