Математическая статистика в горно-геологических расчетах, страница 32

В матричной форме уравнение регрессии имеет вид:  Х×А = У

Умножим обе части уравнения слева на транспонированную матрицу Х^Т.

Получим:  Х^Т×Х×А = Х^Т ×У.  Обозначим матрицу моментов В = Х^Т×Х. Тогда из матричного уравнения  В×А = Х^Т ×У можно найти матрицу оценок:

                                      А = В^–1 × (Х^Т ×У).

Расчет коэффициента детерминации производится по формуле:

    .

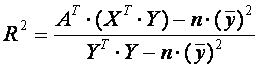Корреляционное отношение находится по формуле:    .

Проверка модели на адекватность осуществляется по критерию Фишера: 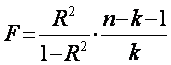     ,  где n  – объем выборки,  k  –  число переменных в уравнении регрессии. Затем по таблице критические точки распределения  Фишера – Снедекора (Приложение 7) находим критическое значение критерия

                                             F_кр = F(a , k₁ , k₂),

где a - значимость ошибки первого рода, k₁ = k , k₂, = n – k –1.

Если наблюдаемое значение критерия F окажется больше критического, то признаем полученную множественную регрессию адекватной;  если  же наблюдаемое значение критерия F окажется меньше критического,  то делаем вывод, что построенная модель не адекватной реальной.

Замечание 1   Данный способ проверки модели на адекватность можно применять и для двумерных как линейных, так и нелинейных моделей.

Замечание 2   Матричный подход в составлении уравнения регрессии можно также использовать  для случая линейной регрессии с одной переменной.

        Рассмотрим пример составления множественной регрессии.

Задача. Исследуется  зависимость месячной добычи угля по участку от мощности разрабатываемого пласта и глубины проведения работ.

Введем обозначения факторов: 

У – месячная добыча угля;  Х₁ – мощность пласта, Х₂ – глубина проведения работ.

Используя физическую сущность факторов, определим зависимые и независимые признаки.

Результативный (зависимый) признак – У ;

независимые признаки –   Х₁   и   Х₂ .

Исходные данные по 20 лавам, работающие примерно в одинаковых условиях, приводятся в таблице: