Пусть событие А – перфоратор оказался нестандартным.
Тогда р = Р(А) является неизвестной вероятностью, которую нужно оценить по выборке и по результатам испытаний и оценки сделать вывод о возможности и условиях сделки.
Запишем исходные данные задачи:
N = 1000; n = 60; m = 6; g = 0,9.
Выборочная доля равна w = 6/60 = 0,1.
Для построения доверительного интервала используем формулу (5), случай с).
Имеем : 2Ф(t) = 0,9. Отсюда Ф(t) = 0,45. По таблице приложения 2 находим t = 1,64. Подставляем в формулу (5) и находим верхнюю и нижнюю границы искомой вероятности:
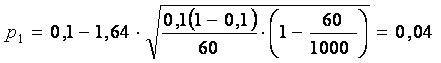
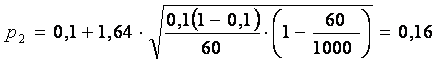
Следовательно, с надежностью прогноза 90% можно утверждать, что процент нестандартной продукции во всей закупаемой партии перфораторов находится в пределах от 4% до 16%. Значит, партию перфораторов можно купить, но при этом потребовать скидку у производителя на 25%.
Гипотеза – это высказывание предположительного характера. Под статистической гипотезой понимают гипотезу о параметрах распределения или виде функции распределения генеральной совокупности.
Примерами статистических гипотез являются следующие высказывания: генеральная совокупность, описывающая мощность пласта угля, имеет нормальный закон распределения или генеральная средняя (математическое ожидание мощности пласта) равна 1 м.
Определение. Статистическая гипотеза называется непараметрической, если в ней сформулированы предположения относительно вида функции распределения.
Определение. Статистическая гипотеза называется параметрической, если в ней сформулированы предположения относительно значений параметров функции распределения известного вида.
Определение. Нулевой гипотезой называют основную гипотезу и обозначают символом Но. Обычно нулевые гипотезы утверждают, что различие между сравниваемыми величинами (параметрами или функциями распределения) отсутствуют, а наблюдаемые отклонения объясняются лишь случайными колебаниями выборки.
Определение. Альтернативной (конкурирующей) называется гипотеза, конкурирующая с нулевой гипотезой в том смысле, что если нулевая гипотеза отвергается, то принимается альтернативная, которую обозначают символом Н1 .
Проверку статистических гипотез обычно осуществляют в следующем порядке:
А) Располагая выборочными данными х1, х2, …, хn и руководствуясь конкретными условиями рассматриваемой задачи, формулируют гипотезу Н0, которую называют основной или нулевой, и конкурирующую гипотезу Н1 . Конкурирующая гипотеза представляет собой ту гипотезу, которая будет принята, если отвергнут основную гипотезу.
Б) Задаются вероятностью a, которую называют уровнем значимости ошибки первого рода. Поясним ее смысл. Решение о том, можно ли считать высказывание Н0 справедливым для генеральной совокупности, принимается по выборочным данным, т.е. по ограниченному ряду наблюдений, следовательно, это решение может быть ошибочным. При этом может иметь место ошибка двух родов: отвергают гипотезу Н0, или, иначе, принимают альтернативную гипотезу Н1, тогда как на самом деле гипотеза Н0 верна – это ошибка первого рода; принимают гипотезу Н0, тогда как на самом деле высказывание Н0 неверно, т.е. верной является гипотеза Н1 – это ошибка второго рода.
Значит, уровень значимости a - это вероятность ошибки первого рода, то есть вероятность того, что верная основная гипотеза будет отвергнута и принята ошибочная конкурирующая гипотеза.
В). Вводят статистический критерий проверки сформулированных гипотез, который представляет собой случайную величину, подчиняющуюся определенному заранее известному закону распределения, если верна основная гипотеза. По уровню значимости ошибки первого рода строят допустимую область (где принимается гипотеза Н0) и критическую область где отвергается гипотеза Н0 и принимается гипотеза Н1).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.