Математическая статистика в горно-геологических расчетах, страница 33

В данной задаче объем выборки равен n = 20.

Число независимых переменных равно k = 2.

Уравнение линейной регрессии имеет вид:

Расчеты осуществим  при помощи пакета программ Mathcad.

Реализация расчетов всех необходимых параметров и характеристик данной задачи в среде Mathcad демонстрируется ниже.

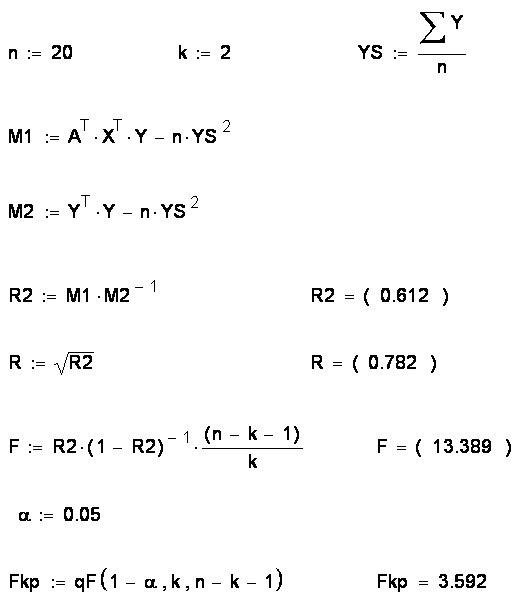
Используя результаты расчетов, сделаем выводы.

1) Уравнение линейной регрессии имеет вид:

Значит, с увеличением мощности пласта (Х₁)  месячная добыча угля увеличивается,  а  с  увеличением глубины работ (Х₂) месячная добыча угля уменьшается.

2) Коэффициент детерминации равен R² = 0,612. Следовательно,  вариации признаков Х₁    и  Х₂  объясняют  61,2%  общей дисперсии результативного признака  У. Остальная часть дисперсии У (38,8%) объясняется другими факторами, неучтенными в данной модели. Пользуясь шкалой Чеддока, можно утверждать, что между месячной добычей угля и независимыми факторами, такими как мощность пласта и глубина проведения работ существует заметная связь.

3) Корреляционное отношение для линейной множественной модели равно

                            R = 0,782.

4)  Проверка модели на адекватность по критерию Фишера при уровне значимости ошибки первого рода a = 0,05 подтверждает адекватность модели, так как  наблюдаемое значение критерия F=13,389 больше критического значения  F_кр = 3,592.

5.9 Оценка погрешности модели 

          Сравнение различных моделей производится по следующим позициям:

·  по коэффициентам детерминации (теоретическим) и сравнение их с эмпирическим коэффициентом детерминации. Чем больше коэффициент R²_теор и чем ближе он к R²_эмпир, тем представленное уравнение регрессии лучше описывает зависимость между признаками Х и У.

·  По средней относительной погрешности аппроксимации:

                                                         (11)

 где  y_i^теор – индивидуальные значения результативного признака У, рассчитанные  по уравнению регрессии: y_i^теор=f(x_i);  у_i – значения признака У из выборки. Чем меньше средняя относительная  погрешность аппроксимации, тем модель лучше описывает зависимость между признаками. Для качественной оценки модели по относительной  погрешности аппроксимации используют следующую шкалу:

·  По средней квадратической погрешности уравнения:

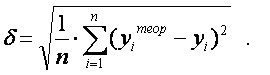                                                        (12)

Для расчета перечисленных характеристик нужно после того, как было получено уравнение регрессии (линейное или нелинейное), заполнить следующую таблицу: