Математическая статистика в горно-геологических расчетах, страница 12

где   х₀ – начало модального интервала;

         n_Mo – частота модального интервала;

         n_{Mo -1} – частота интервала, предшествующего модальному;

         n_{Mo +1} – частота интервала, следующего за  модальным;

        h – величина модального интервала.

Медиана вычисляется по формуле:

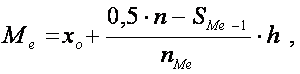
где   х₀ – начало медианного интервала;

         n_Mе – частота медианного интервала;

         n – объем выборки;

         S_{Me -1} – накопленная частота интервала, предшествующая медианному;

        h – величина медианного интервала.

2.3    Метод  “условного нуля”

 Если выборка представлена статистическим рядом с равноотстоящими вариантами или интервальным статистическим рядом с равными интервалами разбиения, то целесообразно для упрощения расчетов использовать метод  “условного нуля”. В этом случае выбирают в качестве  “условного нуля” одну из вариант С, стоящую в центре ряда и имеющую наибольшую частоту.  Затем переходят к условным вариантам по формуле  u_i = (x_i –C)/h и заполняют специальную таблицу.

Таблица 6.

Для проверки правильности вычислений используется тождество: ån_i(u_i+1)² = ån_iu_i² + 2ån_iu_i + n  .

Из таблицы находятся условные моменты:

М₁ = ån_iu_i / n  ;      М₂ = ån_iu_i² / n .

Выборочная средняя равна:  = М₁·h + C