ёКЕРЧЕНСКИЙ ГОСУДАРСТВЕННЫЙ МОРСКОЙ ТЕХНОЛОГИЧЕСКИЙ УНИВЕРСИТЕТ
КАФЕДРА
ВЫСШЕЙ МАТЕМАТИКИ И ФИЗИКИ
высшая математикА
КОНСПЕКТ ЛЕКЦИЙ
для направления 6.040106 – «Экология, охрана окружающей среды и сбалансированное природопользование»
Керчь 2008 г.
Автор (составитель): Ершова Т.Г., ст. преподаватель кафедры высшей математики и физики КГМТУ
Конспект лекций рассмотрен и одобрен на заседании кафедры ВМ и Ф КГМТУ,
протокол № 2 от « 10 » октября 2008 г.
![]() Керченский
государственный морской технологический университет
Керченский
государственный морской технологический университет
МАТРИЧНОЕ ИСЧИСЛЕНИЕ
1. Определители
Определение Матрицей называется прямоугольная таблица из чисел или иных математических объектов, расположенных в m строках и n столбцах.
Обозначают
матрицы А, В, С, … Общий вид матрицы 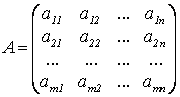 , где aij
– элемент матрицы А, i – номер строки, j – номер
столбца, в которых расположены aij. Выражение
, где aij
– элемент матрицы А, i – номер строки, j – номер
столбца, в которых расположены aij. Выражение ![]() называется размерностью матрицы.
называется размерностью матрицы.
Если m ≠ n – матрица А прямоугольная;
m = n – матрица А квадратная и число n – её порядок;
m = 1 – матрица А есть матрица-строка;
n = 1 – матрица А – матрица-столбец.
Примеры матриц разной размерности, числовых и нечисловых
Квадратная матрица имеет главную и побочную диагонали. Главную диагональ составляют элементы с одинаковыми индексами: а11, а22, …, аnn.
Квадратная матрица, все элементы которой над главной или под главной диагональю – нули, называется матрицей треугольного вида. Примеры
Диагональная матрица – квадратная матрица, все элементы которой – нули, кроме элементов главной диагонали. Примеры
Единичная матрица – диагональная матрица, на главной диагонали которой стоят единицы. Обозначается чаще всего Е.
Ноль-матрица – матрица любой размерности, все элементы которой нули.
Все квадратные матрицы имеют специальную характеристику – определитель.
Определение Определителем матрицы А называется число или математическое выражение, получаемое из элементов данной матрицы А по определенному правилу.
Обозначение
![]() .
.
Примеры 1) матрица А 2-го порядка и ее определитель;
2) матрица В 3-го порядка и ее определитель.
Пусть А – квадратная матрица n-го порядка.
Определение
Минором Mij элемента
aij матрицы
А называется определитель (n – 1)-го порядка, полученной из ![]() вычеркиванием
i-ой строки и
j-го столбца.
вычеркиванием
i-ой строки и
j-го столбца.
Примеры 1)  ;
; 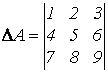 .
Указать миноры элементов а12, а31.
.
Указать миноры элементов а12, а31.
а12
= 2; ![]() ;
а31 = 7;
;
а31 = 7; ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.