Конспект лекций по дисциплине "Высшая математика", страница 3

5. Если в определителе поменять местами два соседних ряда, то определитель изменит знак на противоположный. Пример

6. Если к элементам какого-либо ряда прибавить элементы другого ряда, умноженных на число, то определитель не изменится.

Пример   

Говорим, что линейные операции над строками (столбцами) определителя не изменяют его величину.

7. Определитель треугольного вида и определитель диагонального вида равен произведению элементов, стоящих на главной диагонали:

.

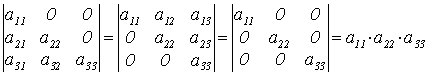Если определитель равен нулю, без явных внешних признаков, то любая его строка (столбец) есть результат линейных преобразований с остальными строками (столбцами) или говорим, что любая его строка (столбец) есть линейная комбинация остальных строк ( столбцов), т.е. определитель имеет несамостоятельную (зависимую) строку (столбец).

Математические операции над матрицами

1. А = В, если А и В имеют одинаковые размерности и равны их одноименные элементы .

2. , при сложении (вычитании) матриц одинаковой размерности складываются (вычитаются) одноименные элементы.

3. , при умножении матрицы А на число α каждый элемент матрицы умножается на это число.

Следствие  Если все элементы матрицы имеют общий множитель, то его можно вынести за знак матрицы, как сомножитель.

Операции 1, 2, 3 называются линейными операциями над матрицами.

Свойства линейных операций

1) А + В = В + А (коммутативность);

2) (А + В) + С = А + (В + С) (ассоциативность);

3) α (А + В) = αА + αВ (дистрибутивность);

4) А + 0 = А.

4. , перемножаются только согласованные матрицы.

Определение   Матрицы А, И называются согласованными на произведение , если число столбцов первого сомножителя А равно числу строк второго сомножителя В.

Правило перемножения матриц :

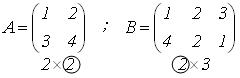Каждый элемент С_ij матрицы С равен сумме парных произведений элементов i-ой строки матрицы А на соответствующие элементы j-го столбца матрицы В, т.е. перемножение производится по правилу «строка на столбец». Матрица С будет иметь столько строк, сколько имеет матрица А, и столько столбцов, сколько имеет матрица В.

Примеры   1)                                       

,

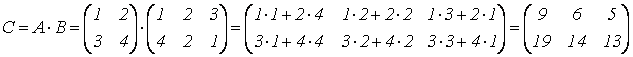размерность .

Операция перемножения матриц в общем случае некоммутативна . Умножение матрицы на единичную матрицу коммутативно.

5. Обращение матрицы

Определение   Квадратная матрица, определитель которой равен нулю, называется вырожденной. В противном случае матрица невырожденная.

Всякая невырожденная матрица А имеет обратную матрицу А^-1.

Определение   Матрица А^-1 называется обратной к матрице А, если от умножения на нее слева и справа получается единичная матрица , т.е. .