Конспект лекций по дисциплине "Высшая математика", страница 29

(Основные теоремы о конечных пределах)

1. Пусть функции  и  имеют конечные пределы при  (или при ), т.е. , .

Тогда  а) ;

б) ;

в) , если .

2) Если  и  при  (или при ) имеют равные пределы  и  и выполняется неравенство , то .

3. Если при  (или при ) функция  принимает неотрицательные значения  и при этом , то число .

4. Если при  (или при ) , то .

5. Если  – возрастающая функция и ограниченная, т.е. , то она имеет предел , где .

Следствия  Пусть ,  .

1. .

2. .

3. .

4. .

5. .

Определение  Выражения вида    называются неопределенными выражениями или неопределенностями.

Правило вычисления предела функции:

Для вычисления  необходимо в формулу функции подставить предельное значение аргумента  и вычислить. Если получили конечное число, то предел найден. Если получили одну из неопределенностей, то ее необходимо раскрыть.

Некоторые методы раскрытия неопределенностей

1. В числителе и знаменателе функции выделяются сомножители, приводящие, к неопределенности, которые взаимно сокращаются.

Примеры:  1) .

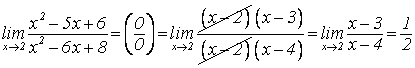2) 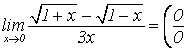; умножим числитель и знаменатель на сопряжение к числителю, т.е. на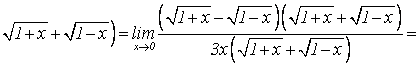 

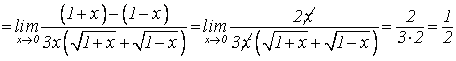.   Примеры

2. Первый замечательный предел:

 ,  , где α – конечное действительное число.  С его помощью вычисляются пределы тригонометрических функций.