Конспект лекций по дисциплине "Высшая математика", страница 14

Уравнение прямой L вида  называется общим уравнением прямой на плоскости.

Геометрический смысл коэффициентов А, В при неизвестных: А, В - координаты вектора нормали  данной прямой.

Неполные уравнения прямой

1)  – прямая проходит через т.О(0,0).

2)  – прямая параллельна оси ОХ (горизонталь).

3)  – прямая параллельна оси ОУ (вертикаль)

4) А = 0;  С = 0;  Ву = 0,  у = 0 – ось ОХ.

5) В = 0;  С = 0;  Ах = 0;  х = 0 – ось ОУ.

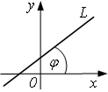2.2. Прямая с угловым коэффициентом

Определение Угловым коэффициентом k прямой Lназывается тангенс угла наклона φ прямой к оси ОХ. .

Определение Любой вектор , параллельный прямой L или расположенный на ней, называется направляющим вектором прямой.

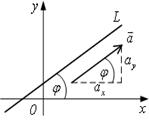Направляющих векторов прямая L имеет много, они между собой коллинеарны.

 ;  ;  ; 

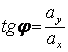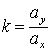
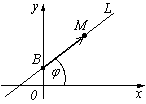т.В(0, b);  т.М(х,у) – текущая точка линии L;  – направляющий  вектор прямой L. Тогда  отсюда  – уравнение прямой с угловым коэффициентом.

Геометрический смысл:  ,  φ – угол наклона прямой к оси ОХ; b – отрезок, отсекаемой прямой по оси ОУ.

Замечание  ;  , тогда вектор , т.к. ; ; .

2.3.Прямая, проходящая через заданную точку М₀(х₀, у₀) с заданным угловым коэффициентом k (пучок прямых)

Пусть .т., тогда ее координаты удовлетворяют уравнению прямой: . Вычтем из уравнения    полученное уравнение : . Это уравнение и называется уравнением пучка прямых с центром в т..

2.4. Прямая через две заданные точки М₁(х₁, у₁), М₂(х₂, у₂)

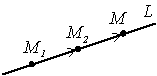Пусть точки на прямой L имеют координаты      т.М₁(х₁, у₁), т.М₂(х₂, у₂), т.М(х, у);  вектор  коллинеарен вектору , следовательно, их одноименные координаты пропорциональны: ; .