Конспект лекций по дисциплине "Высшая математика", страница 4

Определитель матрицы А и ей обратной А^-1 взаимообратны, .

Правило обращения матрицы А, n = 3.

;  .

, А_iJ – алгебраические дополнения к элементам а _iJ матрицы А.

Примеры   1) ; .

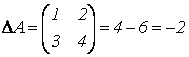Найдем все алгебраические дополнения

;      ;

;   .

;   Проверка:  .

2) ;   .

;        ;   ;

;  ;    ;

;     ;  ;

.

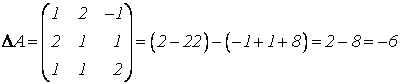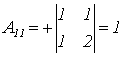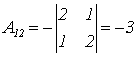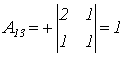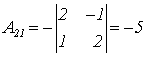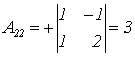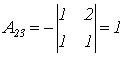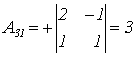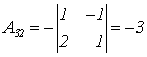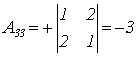Проверка:  

.

СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ

Решение линейных систем

Определение   Системой линейных алгебраических уравнений (СЛАУ) называется система вида 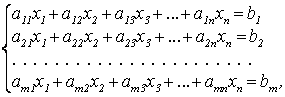                             (1)

где 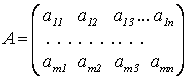 состоит из коэффициентов при неизвестных, a_ij – действительные числа и называется матрицей системы (1); ΔА называется определителем системы.

– столбец свободных членов, bi – действительные числа;

– столбец неизвестных.

Определение  Решением СЛАУ (1) называется совокупность чисел           (α₁, α₂,..., α_n), которые, будучи подставлены в каждое уравнение системы (1), обратят каждое уравнение в тождество.

СЛАУ(1) называется совместной определенной, если решение единственное, т.е. совокупность чисел (α₁, α₂, …, α_n) одна.

Если решение не одно (в этом случае их бесконечно много), то СЛАУ(1) называется совместной неопределенной.

Если СЛАУ(1) не имеет решений, то система называется несовместной.

Если все свободные члены b_i = 0, то СЛАУ(1) называется однородной, в противном случае СЛАУ(1) неоднородная.

Решение линейных систем

1. Правило Крамера решения СЛАУ(1) (m = n,  ΔA ≠ 0)

Рассмотрим квадратную систему вида (1) третьего порядка, определитель которой :