Конспект лекций по дисциплине "Высшая математика", страница 35

6.

,     . Доказывается аналогично п.5.

7.  – сложная функция;  – промежуточная переменная,

х – аргумент. Тогда  .

Доказательство: пусть  и  – дифференцируемые функции. Если аргумент х получит приращение , то переменная и получит соответствующее приращение , которое в свою очередь влечет изменение функции у на величину .

 (при , ) . Следовательно, .

8. Пусть  и  – две взаимно обратные функции, дифференцируемые в точке . Пусть существует  (при , , т.к.  дифференцируема в т.) 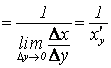;  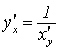 при .

Таблица основных производных

(Формулы дифференцирования)