Конспект лекций по дисциплине "Высшая математика", страница 23

;    ;  , следовательно, .

В качестве опорной точки возьмем точку пересечения этой прямой с какой-нибудь координатной плоскостью, например, XOY:

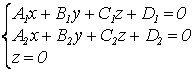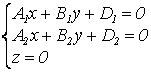  ;    ,  в результате решения СЛАУ получим т. М₀(х₀, у₀, 0).

6. Взаимное расположение прямой L и плоскости Р

1) , тогда  и  или .

2) , тогда  и .

3) Точка пересечения L и P. Удобнее всего уравнение прямой взять в параметрическом виде, уравнение плоскости Р в общем виде. Получим систему:

Неизвестным является параметр t. Имеем фактически одно уравнение с одним неизвестным . Решив уравнение, получим значение параметра t для точки пересечения

L и P. Далее найдем координаты x, y, z этой точки.

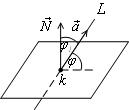4) Угол φ между прямой L и плоскостью Р.

;  ;  ;

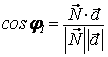.  Следовательно, .

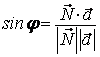7. Взаимное расположение двух прямых в пространстве

1) , следовательно,  .

2) , следовательно,  и .

3) Угол φ между L и L₂ найдем по формуле .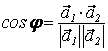

Примеры

математический  анализ

Пусть даны два непустых числовых множества  и .

Определение  Если любому значению  по определенному закону (или по правилу) поставлено в соответствие некоторое значение , то говорят, что задана функция у от х.

Обозначается:  или .

Если значению  соответствует по формуле  одно значение , то функция называется однозначной; в противном случае – многозначной. Переменная х называется независимой переменной или аргументом, переменная у называется функцией.

Определение  Областью определения функции  называется совокупность всех тех значений х, для которых функция  вычисляется конечным действительным числом (или определена, или существует).