Конспект лекций по дисциплине "Высшая математика", страница 2

2) . Указать минор элемента а₂₂.   а₂₂ = 4;   М₂₂ = 1.

Определение  Алгебраическим дополнением А_ij элемента а_ij матрицы А называется выражение вида  .

Примеры  1)

Указать алгебраические дополнения элементов а11, а32.

а₁₁ = 1;    ;    .

а₃₂ = 8;    ;    .

2)  . Указать алгебраическое дополнение элемента а₂₁.

а₂₁.=3;    М₂₁ = 2;    .

Будем называть рядом определителя (матрицы) строку или столбец определителя (матрицы).

Правило вычисления определителя любого порядка

Теорема Лапласа  Определитель матрицы А n-го порядка равен сумме парных произведений элементов любого ряда на свои алгебраические дополнения.

Рассмотрим частные случаи.

1. Определитель 2-го порядка

Δ имеет 2 строки и 2 столбца, следовательно, имеется 4 возможности вычислить Δ.

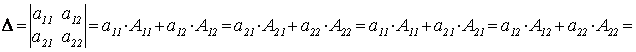
найдем все алгебраические дополнения;  .

Итак, 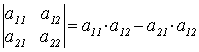, т.е. определитель 2-го порядка равен произведению элементов по главной диагонали минус произведение элементов по побочной диагонали.

2. Определитель 3-го порядка

В данном случае можно вычислить определитель, раскрывая его по любой строке или любому столбцу (6 возможностей).

 (по первой строке)

                .

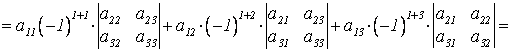
Частный случай – правило треугольников; рассм. на практическом занятии.

Пример 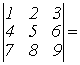   (раскроем по третьему столбцу) =

Свойства  определителей

Определение  Операция, при которой каждая строка определителя (матрицы) становится соответствующим по номеру столбцом, называется транспонированием.

1. Транспонирование не изменяет величины определителя. Пример

2. Если все элементы какого-либо ряда определителя – нули, то определитель равен нулю. Пример

3. Если все элементы какого-либо ряда определителя имеют общий множитель, то его можно вынести за определитель. Пример

Следствие  Чтобы умножить определитель на число, достаточно умножить на это число все элементы какого-либо ряда. Пример

4. Если определитель содержит два одинаковых или два пропорциональных ряда, то определитель равен нулю. Пример