Конспект лекций по дисциплине "Высшая математика", страница 24

Областью значений функции  называется совокупность всех значений, принимаемых переменной у.

Способы задания функции :

1) аналитический – способ задания функции с помощью формул. Если уравнение, с помощью которого задается функция, разрешено относительно у, то функция называется явно заданной, в противном случае – неявно заданной.

Примеры

При аналитическом способе задания функции встречаются случаи, когда функция задана не одной, а несколькими формулами. Примеры

2) Табличный – способ задания функции при помощи таблицы. Например, таблицы тригонометрических функций, логарифмы и т. п. Табличный  способ широко используется в экспериментах и наблюдениях. Недостатком табличного способа является то, что функция задается не для всех значений аргумента.

3) Графический – способ задания функции при помощи графика.

График функции  – множество точек (х; у) плоскости ХОУ, координаты которых связаны соотношением . Само равенство  называется уравнением этого графика.

Например, для измерения атмосферного давления на различных высотах используют барограф, который на движущейся ленте записывает в виде кривой линии изменение давления в зависимости от высоты.

4) Программный – способ задания функции в виде программы на компьютере.

5) Задание функции в виде рядов Тейлора, Маклорена, Фурье и т. п.

Классификация основных элементарных функций

1. Линейная функция у = ах + в, ее график – прямая линия.

2. Квадратичная функция , ее график – парабола.

3. Многочлен или целая рациональная функция , где А_i – коэффициенты многочлена, конечные действительные числа; n – натуральное число, называемое степенью многочлена.

Эта функция определена при всех значениях х. Линейная и квадратичная функция есть частный случай многочлена. Обозначается многочлен .

4. Рациональная дробь определяется как отношение двух многочленов:

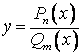   или   .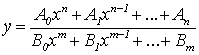

Рациональная дробь определена при всех х, кроме тех, при которых знаменатель обращается в ноль.

Пример   – обратная пропорциональная зависимость между х и у. Графиком этой функции является гипербола, отнесенная к осям координат.

5. Степенная функция , α – действительное число. Область определения этой функции: х – любое, если α – натуральное число; , если α - целое отрицательное число; , если α – произвольное действительное число.

6. Показательная функция , , , определена при всех значениях х.

Частный случай  (экспонента). Примеры : графики.

7. Логарифмическая функция , , , определена при .