Конспект лекций по дисциплине "Высшая математика", страница 8

Вектор, противоположный вектору , обозначается «–». Для вектора  противоположным будет .

Определение   Орт – единичный вектор любого направления .

Обозначается  или . Длина орта равна единице, . Тогда .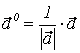

Примеры   1)                                   ;    

Определение   Углом φ между векторами   и  называется наименьший  угол, на который надо повернуть один вектор до его совпадения с другим, если привести оба вектора к общему началу.

Определение   Компонентой вектора  по оси ОХ называется вектор , где т.А₁ – проекция  т.А,  т.В₁ – проекция т.В на ось ОХ.

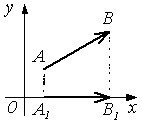Проекцией  на ось ОХ называется длина его компоненты  по оси ОХ, взятая со знаком «+», если направление  и оси ОХ совпадают, и со знаком «–», если они противоположны. Обозначается проекция пр_х . Аналогично определяются проекции вектора на оси ОУ и ОZ, обозначаются соответственно пр_у  и пр_z . Чтобы найти проекции вектора, заданного двумя точками, необходимо из координаты конца вектора вычесть одноименные координаты начала. Проекции вектора на ось OX, OY, OZ называется его координатами.

Примеры   Свойства проекций векторов на ось l, где l обозначает одну из осей OX, OY или OZ:   1)

                            2)

                            3)

                            4) равные векторы имеют равные проекции.

Можно записать  , его длина .

Если  задан в пространстве, то  и его длина

Вектор может быть задан в координатах на плоскости или в пространстве:  или . Числа а_х, а_у, а_z – проекции вектора  соответственно оси OX, OY, OZ. При построении вектора в качестве точки приложения берут начало координат т. О. В этом случае длина вектора  на плоскости и   в пространстве.