Конспект лекций по дисциплине "Высшая математика", страница 39

Определение  Точка  называется точкой максимума функции , если существует такая окрестность точки , что для любого х из этой окрестности  .

Точка  называется точкой минимума функции , если для любого х из некоторой окрестности точки  .

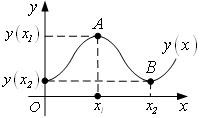
Максимум  или минимум   называется экстремумом функции. Это точечное (локальное) понятие. Экстремум  может достигаться лишь внутри области определения . Граничные точки области определения не могут быть точками экстремума . На приведенном рисунке.  достигает  в точке  и  в точке .

Если исследуемая на экстремум функция  дифференцируема, то изучение свойств  дает возможность находить точки экстремумов.

Необходимое условие существования экстремума

Если точка  – точка экстремума , то

1) , т.е. первая производная равна нулю в этой точке или

2)  не существует.

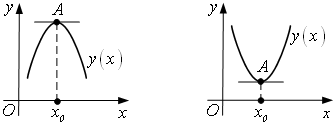Примеры  1.

В точках экстремума касательная к  , т.е. .

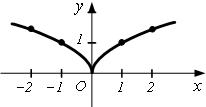2. Пусть ;  ;  при    не существует; касательная к  в точке   перпендикулярна оси ОХ. Точка  – точка  функции .

Непрерывная функция  может иметь экстремум только в точках, в которых  или  не существует. Такие точки называются критическими по  или критическими I рода, они принадлежат области определения  и отделяют интервалы монотонности друг от друга.

Достаточные условия существования экстремума

Пусть  определена и непрерывна в точке  и  или  не существует.