Конспект лекций по дисциплине "Высшая математика", страница 10

2) ;  ;  .

;   – разложение вектора  по базису .

Для любого вектора на плоскости существует единственное разложение по координатному базису , где  – координаты вектора .

Аналогично, для вектора  в пространстве имеем .

При сложении (вычитании) векторов, заданных в координатной форме, получаем вектор, координатами которого будет сумма (разность) одноименных координат слагаемых векторов:

1)

            .

2)

            .

3) При умножении на число λ вектора , заданного в координатах, каждая координата  умножается на это число:

.

4) Равные векторы имеют равные координаты. Аналогичный результат можно получить, используя свойства проекций.

Пусть векторы  и  коллинеарны и , тогда ;  ;  . Отсюда следует условие коллинеарности векторов: 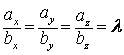 , т.е. одноименные координаты коллинеарных векторов пропорциональны.

Чтобы найти орт  вектора , заданного в координатах, необходимо каждую координату  умножить на число :  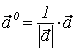;  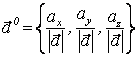.  Учитывая определение направляющих косинусов, можно записать .

Определение   Радиусом-вектором т.М называется вектор, соединяющий начало координат т.О с т.М, т.е.  . Его координаты совпадают с координатами т.М.

На плоскости ; в пространстве .

Примерыпостроения  , вычисление его длины и направления.

Определение   Вектор  называется линейной комбинацией векторов  .

Примеры    Найти длину вектора , если ; .

Скалярное произведение векторов

Определение  Скалярным произведением двух векторов  и называется произведение их модулей на косинус угла между ними:   .