Конспект лекций по дисциплине "Высшая математика", страница 11

Так как проекция вектора  на вектор  равна  и проекция  на  равна , то скалярное произведение можно записать в виде: . Отсюда   и ;.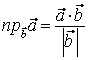

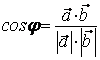Свойства скалярного произведения

1. ;

2. ;

3. .

Скалярное произведение вектора  на себя называется скалярным квадратом: ; .

Скалярный квадрат вектора равен квадрату его модуля.

Тогда  ;  ;  . Если  , то  и наоборот.

Следовательно, условие перпендикулярности векторов: .

Тогда ;  ;  .

Найдем скалярное произведение векторов, заданных в координатной форме. Пусть ,  , тогда  .

Скалярное произведение в координатной форме равно сумме парных произведений одноименных координат векторов.

Физический смысл скалярного произведения:. Работа постоянной силы  на прямолинейном пути  равна скалярному произведению вектора силы  на вектор перемещения .

Примеры отыскания скалярного произведения, угла φ, проекций векторов, работа силы, проверки перпендикулярности векторов и т.п.

Векторное произведение векторов

Определение   Тройка некомпланарных векторов  называется правой (+), если кратчайший поворот от  к из конца оси  виден против часовой стрелки, в противном случае, тройка называется левой (–).

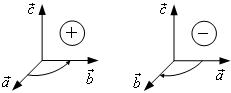Координатные орты () составляют правую тройку векторов, система координат в этом случае называется тоже правой.

Определение   Векторным произведением  на  называется вектор , обозначаемый символом  и удовлетворяющий условиям: