Конспект лекций по дисциплине "Высшая математика", страница 17

Отрезок B₁B₂ = 2b называется (при а > b) малой осью эллипса;  – малая полуось эллипса.

3. ;  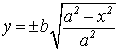 ;     и существует, если   или  ,   (от А₁  до А₂).

;    и существует, если   (от В₁  до В₂).

Кривая расположена в прямоугольнике  А₁В₁А₂В₂.

4. Степень вытянутости эллипса определяет параметр – эксцентриситет:

   или   ,   .

Если a = b, то имеем окружность с центром в т.О(0;0) и радиуса а. В этом случае .

Если , то имеем отрезок А₁А₂ и . Эллипс (при ) получен равномерным сжатием окружности сверху – снизу.

Аналогично можно рассмотреть случай, когда фокусы F₁F₂ расположены на оси ОУ ().

Пример: построение эллипса по каноническому уравнению и отыскание его параметров...

б) Смещенный эллипс

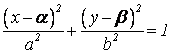 – уравнение смещенного эллипса. Центр расположен в        т. С(α;β).

При построении смещенного эллипса применяется преобразование системы координат – параллельный перенос.

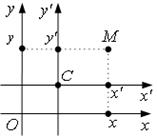ХОУ – старая система координат;

т.О(0;0) – начало координат;

Х'СУ' – новая система координат; т.С(α,β) – ее начало координат.

, , масштабная единица одна и та же.

Возьмем на плоскости произвольно т.М. В системе ХОУ ее координаты х,у; в системе Х'СУ' – х',у' , причем ; . Отсюда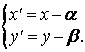 

Сделаем в уравнении смещенного эллипса замену переменной по формулам 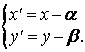, получим каноническое уравнение эллипса .

Строим эллипс по его каноническому уравнению в системе Х'СУ'.

Пример: построение эллипса, заданного в смещенном виде:  .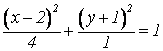

3.3 Гипербола – ГМТ плоскости, модуль разности расстояний которых до двух фиксированных точек плоскости – фокусов F₁, F₂ – постоянен и равен   числу 2а.

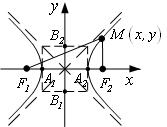а) Каноническое уравнение

Выбор системы координат: ось ОХ проходит через фокусы F₁, F₂; ось ОУ – срединный перпендикуляр к отрезку F₁F₂, называемому фокусным расстоянием F₁F₂ = 2с.