Конспект лекций по дисциплине "Высшая математика", страница 28

           3)  – бесконечно малая при ;

           4)  – бесконечно малая при .

Определение  Функция  называется бесконечно большой при  или при , если  или .

Из определения предела следует, что если, например , то это значит, что бесконечно большая функция не имеет предела в окрестности точки  или неограниченно изменяется при , т.е. для любого числа  существует такое число , что для всех х, удовлетворяющих неравенству , .

Примеры  1)

; функция  при  есть бесконечно большая.

2)   

; функция  является бесконечно большой при .

Свойства бесконечно больших

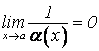1. Величина обратная бесконечно большой при  или при, есть бесконечно малая, т.е. если  или , тогда  или .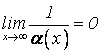

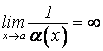2. Величина,  обратная бесконечно малой при  или , есть бесконечно большая, т.е. если  или , тогда  или .

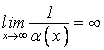Можно доказать:

3.  – есть бесконечно большая;

4.  – бесконечно большая;

5. Сумма двух бесконечно больших одного знака при  или  есть бесконечно большая, чего нельзя сказать о разности двух бесконечно больших. Примеры     1)      2)       3)       4)

Основные свойства конечных пределов