Конспект лекций по дисциплине "Высшая математика", страница 16

Аналогично .

Следствие При делении отрезка пополам  λ = 1, тогда ;   .

Примеры  1. Построение прямой по уравнению, выделить и построить , . Найти , .

2. Привести общее уравнение прямой к виду с угловым коэффициентом и в отрезках и наоборот.

3. Проверить параллельность, перпендикулярность прямых. Найти угол между прямыми и точку пересечения.

4. Найти уравнение высоты, медианы в треугольнике. Найти уравнение прямой, параллельной стороне треугольника, проходящей через указанную вершину. Аналогично, с перпендикуляром.

3. Кривые второго порядка

3.1 Окружность – ГМТ плоскости, равноудаленных на расстояние R от фиксированной точки плоскости – центра.

а) Каноническое уравнение окружности: .

Центр окружности  т. О(0;0), радиус R.

б) Смещенная окружность: .

Центр окружности т. С(α;β), радиус R.

3.2. Эллипс – ГМТ плоскости, сумма расстояний которых до двух фиксированных точек плоскости – фокусов F₁, F₂ – постоянна и равна 2а.

а) Каноническое уравнение эллипса

Выбор системы координат: ось ОХ проходит через точки F₁, F₂; ось ОУ – срединный перпендикуляр к отрезку F₁F₂, называемому фокусным расстоянием.

Пусть F₁F₂ = 2с. Тогда в данной системе координат т. М(х,у) – текущая точка  линии; F₁М, F₂М называются фокальными радиусами т.М.

Геометрическое свойство эллипса: F₁М + F₂М = 2а

;  ;

;

;

;    ;

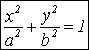;  ;    – каноническое уравнение эллипса.

Свойства эллипса:

1. Уравнение имеет только четные степени х и у; кривая симметрична относительно ОХ и ОУ и относительно начала координат.

Т.О(0,0) – центр эллипса.

2. Точки пересечения эллипса с осями координат:

с ОХ:  . Эллипс пересекает ось ОХ в точках , , называемых вершинами по оси ОХ.

Отрезок  А₁А₂ = 2а называется (при а > b) большой осью эллипса;  – большая полуось эллипса.

с ОУ: . Эллипс пересекает ось ОУ в точках , , называемых вершинами эллипса по оси ОУ.