Конспект лекций по дисциплине "Высшая математика", страница 9

Примеры. Построение вектора по двум точкам, вычисление длины вектора на плоскости и в пространстве.

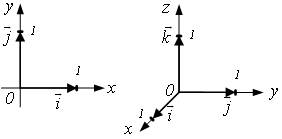
Определение   Координатным базисом на плоскости называется упорядоченная совокупность ортов , приложенных к началу координат О (0, 0) и расположенных на осях ОХ и ОУ соответственно.

В пространстве координатный базис составляет совокупность .

 задают масштабную единицу и указывают направление положительного отсчета. Декартова прямоугольная система координат может быть определена как совокупность фиксированной т.О и базиса.

Определение   Углом между вектором  и числовой осью декартовой системы координат называется угол между  и соответствующим ортом.

Обозначаются углы:

Углы α, β, γ называются направляющими углами вектора .

Направляющие углы вектора можно найти, используя направляющие косинусы: , , ; .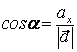

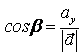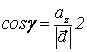Линейные операции над векторами (+, -, )

1.  есть вектор, который находится по правилу параллелограмма, если  приведены к общему началу.

 – диагональ, исходящая из общего начала векторов .

2.  - вторая диагональ параллелограмма, исходящая из конца и входящая в конец  (из конца вычитаемого в конец уменьшаемого).

3.  где λ – действительное число. Длина вектора  направление  совпадает с направление , если , и противоположно, если . Векторы  коллинеарны.

Разложение вектора  по базису

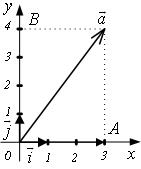 Рассмотрим примеры:

1) Вектор  имеет проекцию на ось ОХ, равную 3, т.е. координата , и проекция  на ОУ равна 4, т.е. координата ; т.о. вектор  .

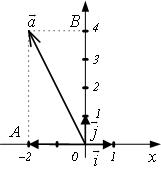С другой стороны  ; ;  и тогда . Коэффициенты при ортах есть координаты . Выражение  называется разложением вектора  по базису .