Конспект лекций по дисциплине "Высшая математика", страница 34

Уравнение касательной к  в :  ;

                                                                                                     k

уравнение нормали к  в :  .

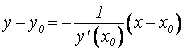Примеры

Теорема (о связи непрерывности и дифференцируемости функции ):

Если функция  дифференцируема в точке х, то она непрерывна в этой точке (без доказательства).

Обратное, вообще говоря, неверно, т.е. существуют функции, непрерывные в точках, но не имеющие в ней , т.е. не имеющие одной касательной к  в этой точке.

Пример  1)   в

2)  в ,  ;  .

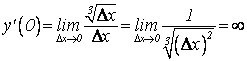При  касательная к  имеет угловой коэффициент , т.е. , следовательно, касательная перпендикулярна к ОХ в т.. В данном случае речь идет о бесконечной производной.

Свойства  (Правила дифференцирования)

1. ;        ;                   ,    .

2. ;         ;             =1; .

3. , где  – дифференцируемая в т. х функция.

                             ;       ;  .

4. , где  и   – дифференцируемая в т. х функция.

                             ;    ; .

5. ;

;

= (если , то , т.к. функция  – дифференцируема в т. х и, следовательно, непрерывна) .