Конспект лекций по дисциплине "Высшая математика", страница 30

Доказательство:  Пусть  – острый угол, т.е.

; .

.

;

;.

Имеем  или . Поделим неравенство на , получим . Переходя к пределу, при  , и используя свойства конечных пределов, получим  и, следовательно, . Перевернем выше полученное неравенство: , т.е.. Переходя в неравенстве к пределу и используя свойства конечных пределов, получим .

Примеры   1) ; 2) ;  3) ;  4) .

Следствие   .

3. Второй замечательный предел

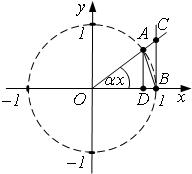
Линия  в т. имеет касательную, для которой угол наклона к оси ОХ , , т.е. угловой коэффициент касательной к = 1.

АВ – хорда (или секущая) линии ;

АС – предельное положение хорды при , т.е. положение касательной;

α – угол наклона хорды АВ к оси ОХ; ;  и тогда .

. Следовательно, .

Основное логарифмическое тождество: , тогда  и .

Имеем две формулы второго замечательного предела: ;

                                                                                             ,

которые используют при раскрытии неопределенности вида .

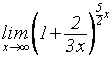Примеры    1) ;    2) ;    3) .

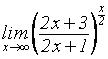4. Третий замечательный предел:

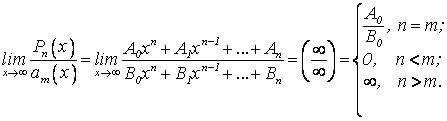          Примеры

Непрерывность функции в точке

Примеры:   1) Пусть аргумент в своем изменении принимает значения

 х: 2,9; 2,99; 2,999; …х→3, находясь слева от 3; говорим х стремится к 3 слева и пишем .