Конспект лекций по дисциплине "Высшая математика", страница 19

б)Смещенная гипербола

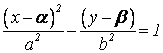. Центр гиперболы расположен в т.. Сделаем параллельный перенос координат в т.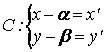, получим уравнение гиперболы в каноническом виде  . Строим гиперболу по каноническому уравнению в новой системе координат .

Аналогично поступаем, если сопряженная гипербола задана в смещенном виде: 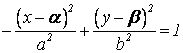   или  .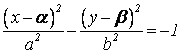

Сделав параллельный перенос, получим каноническое уравнение вида:

  или  .

Пример. Построить линию   .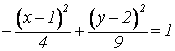

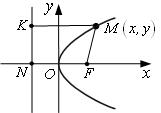
3.4 Парабола – ГМТ плоскости, равноудаленных от фиксированной точки плоскости – фокуса F – и от прямой, называемой директрисой.

а) Каноническое уравнение

Выбор системы координат: ось ОХ – прямая, проходящая через т.F перпендикулярно директрисе и пересекающая директрису в т.N; NF = р. Ось ОУ – срединный перпендикуляр к отрезку NF. В данной системе координат т., т., т. т. - текущая точка линии.

Геометрическое свойство параболы: КМ = FМ.

;   ;

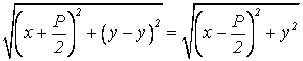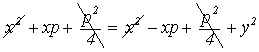 – каноническое уравнение параболы. Вершина расположена в т.О(0,0), ветвь вправо, если , и влево, если . Уравнение директрисы: . Ось ОХ – ось параболы.

Если ось ОY проходит через фокус F параболы перпендикулярно директрисе, ось OX – срединный перпендикуляр к отрезку NF = р, то, проделав преобразования, получим каноническое уравнение параболы в виде х² = 2ру. Вершина расположена в т.О(0,0), ветвь вверх при  и вниз при ; фокус ; директриса имеет уравнение . Ось OY – ось параболы. Парабола симметрична относительно своей оси. Для построения берем несколько точек.

б) Смещенная парабола

  или  .

Вершина расположена в т.В(α; β). Сделаем параллельный перенос системы координат в т.В(α; β) по формулам 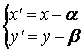 , получим уравнение параболы в каноническом виде:   или  .

Строим параболу в новой системе координат X'ВY'.

Пример. Построить линии:

:  ;  ;  .

3.5 Общее уравнение кривой второго порядка: