3)
Проверить ![]() Р1 :
Р1 : ![]() ; Р2 :
; Р2 :![]() .
.
6. Расстояние от т.M0(x0 , y0 , z0) до плоскостиP: Ax +By+Cz+D = 0
d(т.M0; P)
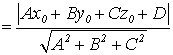 .
.
Примеры 1) Найти длину
перпендикуляра, опущенного из т. А0(1;2;1) на плоскость Р
: ![]() .
.
2)
Найти расстояние плоскости Р : ![]() от
начала координат.
от
начала координат.
7. Геометрический смысл СЛАУ
Если СЛАУ (n = 3) имеет единственное решение, то три плоскости имеют одну точку пересечения.
Если СЛАУ имеет бесконечно много решений, то три плоскости имеют общую линию пересечения.
Если СЛАУ несовместна, то три плоскости не имеют никаких общих пересечений (ни точки, ни линии).
Прямая линия в пространстве
1. Общие уравнения прямой
Прямую
L в пространстве
можно определить как результат пересечения двух плоскостей: 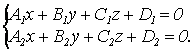
2. Канонические уравнения прямой
Пусть т.![]() и вектор
и вектор ![]() , т.е. является ее направляющим
вектором;
, т.е. является ее направляющим
вектором;
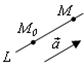 т.
т.![]() и является текущей. Тогда
и является текущей. Тогда ![]() , следовательно,
, следовательно, ![]() . Эти уравнения называются каноническими
уравнениями прямой в пространстве. Точка
. Эти уравнения называются каноническими
уравнениями прямой в пространстве. Точка ![]() называется
опорной точкой прямой. Приведение к общему виду:
называется
опорной точкой прямой. Приведение к общему виду: 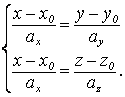
3. Параметрические уравнения прямой
![]() , t
– параметр. Тогда
, t
– параметр. Тогда 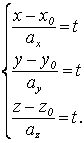 или
или 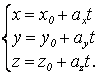
Эти уравнения называются параметрическими уравнениями прямой.
Физический смысл: ![]() – точка начала
прямолинейного движения материальной точки со скоростью
– точка начала
прямолинейного движения материальной точки со скоростью ![]() ;
т.
;
т. ![]() – положение материальной точки в
пространстве в момент времени t.
– положение материальной точки в
пространстве в момент времени t.
4. Прямая, проходящая через две заданные точки
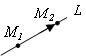 т.
т.![]() – опорная точка
прямой,
– опорная точка
прямой,
вектор ![]() – направляющий
вектор прямой. Тогда уравнения прямой имеют вид
– направляющий
вектор прямой. Тогда уравнения прямой имеют вид
![]() .
.
5. Приведение общих уравнений прямой к каноническому виду
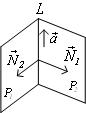
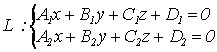 ;
;
![]() ;
; ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.