Проще говоря, линейные преобразования над уравнениями системы не изменяют ее решений.
Рассмотрим метод Гаусса на примерах
1) 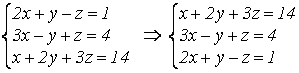
 ;
; 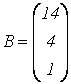 ;
;
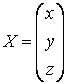 .
.
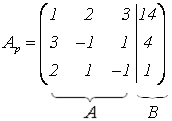 Расширенная
матрица системы
Расширенная
матрица системы
Запишем СЛАУ в виде матричной схемы Гаусса:

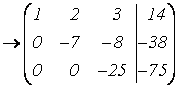 .
.
Прямой ход метода Гаусса закончен. Матрица А свелась к треугольному виду.
Обратный ход метода Гаусса: 3-е уравнение – 25z = – 75;
отсюда z = 3; 2-е уравнение – 7у – 8z = -38; 7у = 14; у = 2;
1-е уравнение x + 2y + 3z = 14; x = 14 – 4 – 9; x = 1.
Решение системы единственное: х = 1; у = 2; z = 3.
2)
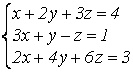 ;
;  .
.
Матрица А свелась к трапецеидальному виду, система имеет противоречивое уравнение 3-е и, следовательно, несовместна.
3)
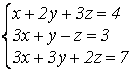 ;
; 
Матрица А свелась к трапецеидальному виду. В системе появилось «пустое» 3-е уравнение. Прямой ход метода Гаусса закончен.
Обратный
ход: 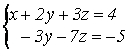 .
.
Имеем
2 уравнения и 3 неизвестных, т.о., одна переменная, например, z свободна,
![]() .
.
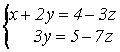 ; отсюда
; отсюда ![]() . Тогда
. Тогда ![]() ;
;
![]() .
.
Данная система
неопределенная, имеет бесконечно много решений: 
Частное решение получаем, задавая конкретное значение z, например, z = 0.
Вывод 1. Правило
Крамера. СЛАУ квадратная (m = n),
невырожденная (Δ ≠ 0). ![]() ;
; ![]() ;
; ![]() .
.
Δ – главный определитель системы; Δх, Δу, Δz – вспомогательные определители.
2. Матричный метод. СЛАУ квадратная, невырожденная. ![]() .
.
3. Метод Гаусса. СЛАУ произвольная. С помощью линейных преобразований над строками в матрице Гаусса последовательно исключаем переменные из уравнений. В результате решения СЛАУ получим один из случаев:
а) матрица А свелась к треугольному виду; решение СЛАУ единственное, находится обратным ходом;
б) матрица А свелась к трапецеидальному виду с противоречивой строкой; СЛАУ несовместна;
в) матрица А свелась к трапецеидальному виду с «пустой» строкой. СЛАУ неопределенная, имеет бесконечно много решений, т. к. появляются «свободные» переменные.
Замечание Однородная СЛАУ всегда совместна, т. к. всегда имеет нулевое (тривиальное) решение. Такие системы решаем точно так же, как и неоднородные.
Пример 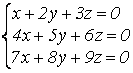 ;
; .
.
Матрица
А свелась к трапецеидальному виду с «пустой» строкой. СЛАУ неопределенная: 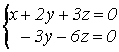 ; у = – 27. х = 7.
Решения СЛАУ:
; у = – 27. х = 7.
Решения СЛАУ: 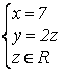 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.