Конспект лекций по дисциплине "Высшая математика", страница 7

Векторная алгебра

1. Декартова прямоугольная система координат на плоскости и в пространстве (ДСК)

Определение  ДСК на плоскости называется совокупность двух взаимно перпендикулярных числовых ориентированных осей ОХ, ОУ и фиксированной точки плоскости, называемой началом координат и обозначаемой т.О.

Числовые оси ОХ и ОУ имеют одинаковую масштабную единицу.

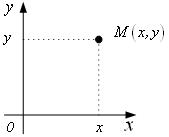
Любая точка плоскости однозначно определяется двумя числами х и у, которые называются координатами точки в данной системе отсчета.

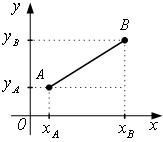
Отрезок АВ определяется двумя точками т.А(х_А,у_А), т.В(х_В,у_В). Длина АВ или расстояние между двумя точками на плоскости определяется по формуле

.

Определение  ДСК в пространстве называется совокупность трех числовых ориентированных взаимно-перпендикулярных осей ОХ, ОУ, ОZ, пересекающихся в      т. О и имеющих одинаковую масштабную единицу.

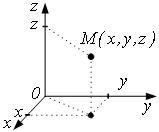
Любая точка пространства имеет три координаты  (x, y, z). Расстояние между двумя точками т. А(x_A, y_A,, z_A) и  т.В(x_В, y_В,, z_В ) находится по формуле:

.

Примеры  построения точек, отрезков на плоскости и в пространстве и отыскания их длин.

2. Векторы

Определение    Скалярной величиной или скаляром называется величина, полностью характеризующаяся своим численным значением. Примеры:температураt, масса m, длина,…

Вектором или векторной величиной называется величина, характеризующаяся численным значением, направлением и точкой приложения.

Примеры:   и т.д.

Если вектор не жестко привязан к точке приложения, то он называется свободным и может перемещаться параллельно самому себе в любую точку приложения. Геометрически векторную величину удобно изображать направленным отрезком. Обозначается вектор: , если задан парой упорядоченных точек, т.А – его начало, т.В – его конец, или .

Модулем вектора (его длиной) называется длина отрезка, изображающего вектор. Обозначается модуль: или .

Определение   Вектор называется нулевым, если его начало и конец совпадают; обозначается . Определенного направления не имеет.

Определение   Векторы называются коллинеарными, если расположены на одной или параллельных прямых. Примеры.

Определение  Векторы называются компланарными, если расположены на одной или параллельных плоскостях.

Равные векторы – коллинеарны, имеют одинаковую длину и одинаково направлены (сонаправлены). В этом случае пишут .

Два коллинеарных вектора (не нулевые), имеющие равные модули, но противоположно направленные, называются противоположными.