Конспект лекций по дисциплине "Высшая математика", страница 20

 – многочлен второго порядка относительно х, у.

 – называется квадратичной формой,

 - линейная форма,  F – свободный член.

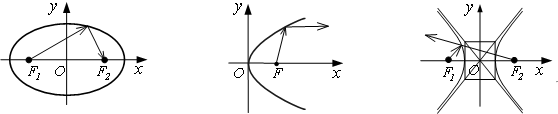
Рассмотрим более простой случай уравнения при В=0; . Выделив полный квадрат по х и у, получим одно из уравнений смещенной кривой. Сделав параллельный перенос системы координат и соответствующую замену переменных в полученном уравнении, получим каноническое уравнение. По каноническому уравнению кривой в новых переменных х', у' строим кривую.

Пример.  Назвать и построить линию:  ;  ;  .

Замечания:

1) Кривая 2-го порядка может вырождаться в пару прямых: ; ;  ,  .

2) Уравнение 2-го порядка может определять одну точку: , точка О(0,0) или окружность нулевого радиуса.

3) Уравнение 2-го порядка может не определять никакого геометрического образа:  (мнимый эллипс).

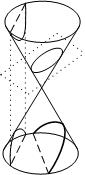
Все кривые 2-го порядка являются коническими сечениями.

Оптические свойства кривых 2-го порядка

1) Если источник света находится в одном из фокусов эллиптического зеркала , то лучи его, отразившись от зеркала, собираются в другом фокусе.

2) Если источник света находится в фокусе параболического зеркала, то лучи его, отразившись от зеркала, идут параллельно оси параболы.

3) Если источник света находится в одном из фокусов гиперболического зеркала, то лучи его, отразившись от зеркала, идут далее так, как если бы они исходили из другого фокуса.

Плоскость Р в пространстве

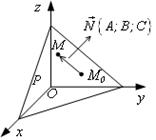1. Общее уравнение плоскости Р

;

вектор  – вектор нормали Р;  и , т. е. . Этот тип уравнения называется связка плоскостей с центром в т.М₀. Раскроем скобки в уравнении и обозначим число, получим общее уравнение плоскости: , где числа А, В, С есть координаты вектора нормали  плоскости Р.

Примеры   1) Найти уравнение плоскости, проходящей через т.М₀(1; 1; -1) и перпендикулярно вектору .

2). Построить плоскость с осями координат.

2. Неполные уравнения плоскости Р

1) , Р проходит через начало координат.

2) , параллельна ОХ;

    А = 0; , Р проходит через ОХ.