Конспект лекций по дисциплине "Высшая математика", страница 41

Достаточные условия существования точки перегиба

Пусть  определена и непрерывна в точке  и  или  не существует.

Тогда, если  изменяет свой знак в окрестности точки , то эта точка есть точка перегиба.

Вывод  1. Найти  и критические точки II рода.

2. О.о.ф. поделится этими точками на интервалы. В каждом интервале найдем знак , взяв одну пробную точку.

3. Укажем точки перегиба и найдем координаты этих точек на плоскости.

4. Асимптоты

1) Вертикальные асимптоты имеют уравнение  и существуют в точках , если хотя бы один односторонний предел  при  бесконечный.

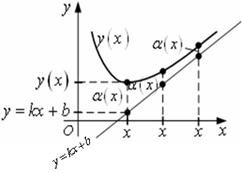2) Наклонные асимптоты имеют уравнение: .

При  ;

; .

Перейдем к пределу при , получим:,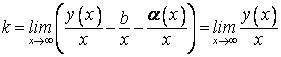

т.к.  и .

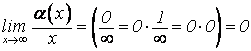Следовательно, . Тогда , т.к. . Следовательно, .

Если k или b бесконечные или не существуют, то наклонных асимптот кривая  не имеет.

Если , то  и кривая  имеет горизонтальную асимптоту, ее уравнение .

5. Четность, нечетность . Периодичность

1) Четность  проверяем по условию . Четные функции симметричны относительно оси ОУ.

2) Нечетность : . Нечетные функции симметричны относительно начала координат О(0,0).

3) Периодичность: .

6. Нули функции и дополнительные точки

Точки пересечения графика  с осями координат называются нулями функции.

1) Пересечение с осью ОХ: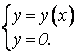

2) Пересечение с осью ОУ: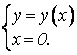

Дополнительные точки вычисляем по некоторым значениям х.

7. График

1)  асимптоты;

2)  характерные точки: экстремумы, перегибы, нули и дополнительные;