Конспект лекций по дисциплине "Высшая математика", страница 21

3) В = 0,   ;

    В = 0,  ,  Р проходит через ОY.

4) C = 0,   ;

    С = 0,  ,  Р проходит через ОZ.

5) А = 0;  В = 0,  .

6) А = 0;  C = 0,  .

7) В = 0,  C = 0,  .

8) x = 0 – уравнение координатной плоскости YOZ;

    у = 0 – уравнение ХOZ;

    z = 0 – уравнение XOY.

3. Уравнение плоскости Р в отрезках

Р:  Ах + Ву + Сz + D = 0;

;  обозначим числа ;  ; , получим плоскость в отрезках: .

Примеры   1) Найти уравнение плоскости Р:   в отрезках и построить Р. Найти углы  с осями координат.

2) Построить плоскости: 2х + 3у – 6 = 0;   3х – 6 = 0;; 2у + 6 = 0;  3х = 0. Указать их нормали.

4. Уравнение плоскости, проходящей через три заданные точки

;

;

.

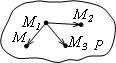
Эти векторы расположены в одной плоскости, следовательно, компланарны, и их смешанное произведение равно нулю.

,  или 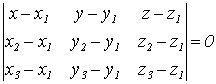 .  Это и есть уравнение плоскости через три заданные точки.

Пример  Найти уравнение плоскости, проходящей через точки М₁(1;2;3); М₂(0;1;1); М₃(-1;-;0). Указать  и найти ее длину.

5. Взаимное расположение двухплоскостей в пространстве

, 

,  .

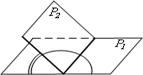
1) , тогда  и, следовательно, .

2) , тогда  и, следовательно, .

3) Углом φ между Р₁ и Р₂ называется любой из двух двугранных углов, образованных этими плоскостями.

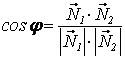
Примеры  1) Найти угол φ между Р₁ : и Р₂ : .

2) Проверить   Р₁ :;  Р₂ :.