Конспект лекций по дисциплине "Высшая математика", страница 38

При этом может  или , или обе переменные  и .

В случае, если  в точке  имеет разрыв II рода, кривая  имеет в этой точке вертикальную асимптоту, ее уравнение .

Примеры:  ;  ;  ;  .

2. Интервалы монотонности функции . Точки экстремумов

Определение   Функция  называется монотонной на  (a; b), если она на интервале на интервале или только убывает, или только возрастает, или постоянна.

Функция  неубывающая на интервале, если она возрастает или постоянна на интервале.

Функция  невозрастающая на (a; b), если она убывает или постоянна на (a; b).

Необходимые условия монотонности функции

Пусть  дифференцируемая на (a; b) функция.

1) Если  на (a; b) не убывает, то  на (a; b).

2) Если  на (a; b) не возрастает, то  на (a; b).

Используем геометрический смысл :  – угловой коэффициент касательной к  в точке х, φ – угол наклона касательной к оси ОХ

Если , то  φ – острый угол, если , то φ – тупой, если , то φ = 0.

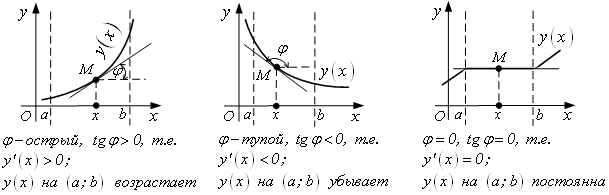Достаточные условия монотонности функции

Пусть  дифференцируема на (a; b).

1) Если  на интервале (a; b), то  возрастает на (a; b).

2) Если  на интервале (a; b), то функция  убывает на (a; b).

3) Если  на интервале (a; b), то функція  постоянна на (a; b).