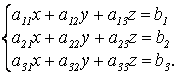Конспект лекций по дисциплине "Высшая математика", страница 5

                                                                         (2)

Правило Крамера: Искомое неизвестное равно дроби, в знаменателе которой стоит главный определитель системы ΔА, в числителе стоит тот же определитель, в котором столбец коэффициентов при искомом неизвестном заменен на столбец свободных членов. Имеем

;   ;   ;   ;

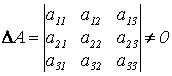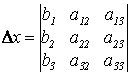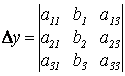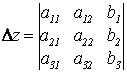 называются вспомогательными определителями.

Тогда  ;  ;   .

Пример

Имеем квадратную систему 3-го порядка, неоднородную. Найдем главный определитель системы.

       .

;

;

;

;   ;   ;

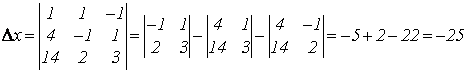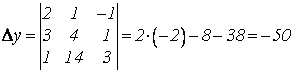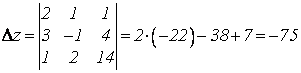Проверка:   2 + 2 – 3 = 1;   3 – 2 + 3 = 4;   1 + 4 + 9 = 14.

2. Матричный способ решения (m = n,  ΔA ≠ 0)

В матричной форме система (1) имеет вид . Умножим уравнение слева на А^-1, получим ; , имеем ,  и окончательно .

Пример  ;  ;  ;  .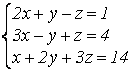

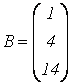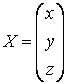матрица А невырожденная и имеет обратную матрицу А^-1.

Найдем все алгебраические дополнения А_ij.

;        ;   ;

;  ;    ;

;     ;  ;

;

; 

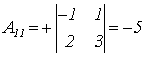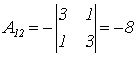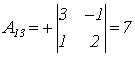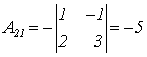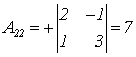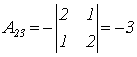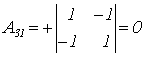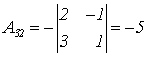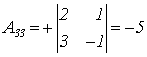3. Метод Гаусса (метод последовательного исключения переменных)

Определение   Системы линейных алгебраических уравнений называются эквивалентными, если они имеют одни и те же решения.

Теорема     Если к какому-либо уравнению системы прибавить любое другое уравнение, умноженное на некоторое число, то вновь полученная система будет эквивалентна исходной.