Конспект лекций по дисциплине "Высшая математика", страница 32

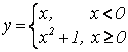Примеры   1) ;    2)  ;    3)

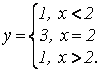
Свойства функций, непрерывных в точке

Пусть ,  и  непрерывны в точке . Тогда непрерывными в точке  будут: 1) ;  2) ;  3) ;

4)  при ;  5) сложная функция , состоящая из непрерывных в точке функций. Доказательство основывается на соответствующих свойствах конечных пределов. Примеры 

Свойства функции , непрерывной на

Определение Функция  называется непрерывной на , если она непрерывна в каждой внутренней точке,  и имеет конечные односторонние пределы , .

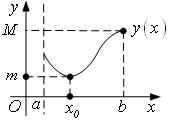
1. Теорема Вейерштрасса

Функция , непрерывная на , достигает на  своего наименьшего (т) и наибольшего (М) значений. , если .

2. Следствие из теоремы Вейерштрасса

Функция , непрерывная на , ограничена на , т.е. существует число  такое, что для   (или ).

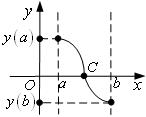3. Если  непрерывна на  и на концах интервала принимает значения  и  разных знаков, то хотя бы в одной внутренней точке интервала  обращается в ноль, т.е. график  пересекает ось ОХ.

;  , существует  и .

Производная функции

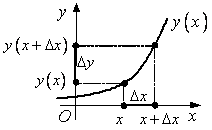Пусть  – приращение аргумента х,

 – соответствующее приращение функции . Отношение   называется средней скоростью функции  на интервале длиной .