Определение Смешанным
произведением векторов ![]() называется скалярное
произведение вектора
называется скалярное
произведение вектора ![]() на вектор
на вектор
![]() .
.
Обозначается ![]() .
.  .
.
Следовательно,
если векторы ![]() компланарны, то
компланарны, то ![]() .
.
аНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ
1. Линия Lна плоскости
Любую линию на плоскости ХОУ будем рассматривать как множество точек, обладающих некоторым геометрическим свойством – геометрическое место точек (ГМТ).
Обозначим: т.М(х,у) – произвольная или текущая точка линии; х,у - текущие координаты; т.М0(х0,у0) – фиксированная точка линии.
Определение
Уравнение ![]() называется уравнением линии L,
если координаты каждой точки линии удовлетворяют этому уравнению, и наоборот,
если координаты какой-либо точки удовлетворяют этому уравнению, то данная точка
принадлежит линии L.
называется уравнением линии L,
если координаты каждой точки линии удовлетворяют этому уравнению, и наоборот,
если координаты какой-либо точки удовлетворяют этому уравнению, то данная точка
принадлежит линии L.
Пример Найти уравнение окружности с центром в т. С (α,β) и радиуса R.
Определение Окружность – ГМТ плоскости, равноудаленных на расстояние R от фиксированной точки плоскости, называемой центром.
Пусть т.М(х,у) – текущая точка окружности и т.С (α,β) – центр окружности.
Геометрическое свойство окружности: ![]() или
или
![]() ;
; ![]() .
Т. о., уравнение смещенной окружности с центром в т.С (α,β) и радиуса R:
.
Т. о., уравнение смещенной окружности с центром в т.С (α,β) и радиуса R:
![]() .
.
Если ![]() , то центр
окружности лежит в т.О(0,0) и уравнение имеет вид:
, то центр
окружности лежит в т.О(0,0) и уравнение имеет вид: ![]() . Такое уравнение называется
каноническим уравнением окружности.
. Такое уравнение называется
каноническим уравнением окружности.
Определение Линия L называется алгебраической линией n-го порядка, если уравнение линии F(x,y) = 0 является многочленом n-го порядка относительно х, у.
Пример
![]() – линия 2-го порядка;
– линия 2-го порядка;
![]() о
– линия 1-го порядка;
о
– линия 1-го порядка;
![]() –
линия 3-го порядка и т.п.
–
линия 3-го порядка и т.п.
Линия L, не являющаяся алгебраической, называется трансцендентной.
Примеры
![]() и т.п.
и т.п.
2. Прямая линия на плоскости
2.1. Общее уравнение прямой
Определение
Любой вектор ![]() , перпендикулярный прямой линии L,
называется ее нормалью.
, перпендикулярный прямой линии L,
называется ее нормалью.
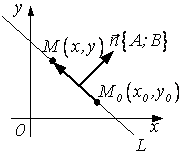 Векторов нормали прямая линия имеет много, они все
коллинеарны.
Векторов нормали прямая линия имеет много, они все
коллинеарны.
Пусть вектор ![]() расположен
на линии L и вектор
расположен
на линии L и вектор ![]() . Тогда их скалярное
произведение равно нулю:
. Тогда их скалярное
произведение равно нулю: ![]() ,
, ![]() ,
, ![]() ;
;
![]() ;
;
![]() ; обозначим
; обозначим ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.