Конспект лекций по дисциплине "Высшая математика", страница 31

Пусть .

Значения :  .

Пишем .

2)  справа, пишем  .

   .

Такие пределы функции носят название односторонних пределов: левосторонний (или левый) предел ; правосторонний (или правый) предел .

Определение 1  Функция  называется непрерывной в точке , если она определена в некоторой окрестности точки   и

1) существуют конечные односторонние пределы  и ;

2) они равны между собой ;

3) и равны значению функции в т. , т.е. . Или коротко: .

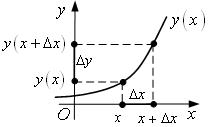
Введем понятие приращения аргумента х и соответствующего приращения функции .

х – исходное значение аргумента;

 – приращенный аргумент;

 – приращение аргумента;

 – исходное значение функции;

 – приращенное значение функции;

п – приращение функции.

Пусть . Обозначим  , тогда   и .

Определение 2  Функция  называется непрерывной в точке , если бесконечно малому приращению аргумента  соответствует бесконечно малое приращение функции . Таким образом, если  непрерывна в точке  , то из  следует .

Определение  Точки, в которых нарушены условия непрерывности функции, называются точками разрыва.

Классификация точек разрыва

1.Если левый предел  или правый , или оба предела бесконечные, то в точке  функция  имеет бесконечный разрыв или разрыв второго рода.

2. Если оба односторонние пределы конечные, но не равные между собой , тогда в точке  функция  имеет конечный  разрыв или разрыв первого рода (скачок).

3. Если , то  в точке  имеет разрыв первого рода, устранимый.