Конспект лекций по дисциплине "Высшая математика", страница 12

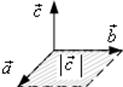
1) , φ – угол между  и ;

2) , ;

3) тройка векторов  образует правую тройку.

Геометрический смысл :   Модуль векторного произведения  численно равен площади параллелограмма, построенного на векторах , , как на сторонах.

Следствие   Площадь треугольника, построенного на векторах , , как на сторонах, равна половине модуля векторного произведения  на , .

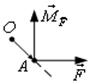
Физический смысл :   Момент силы , приложенной к т. А относительно т.О равен векторному произведению вектора  на вектор силы , . Тройка () должна быть правой. Координаты  вектора  есть моменты этой силы относительно координатных осей.

Свойства :

1)   (антикоммутативность);

2) ;

3) .

Таким образом, векторные многочлены можно перемножать векторно по правилу перемножения алгебраических многочленов, учитывая антикоммутативность.

Пусть ,   . Найдем векторное произведение ортов. , т. к. ; аналогично , .

, действительно,  , ,   и тройка  – правая. Аналогично можно получить  и т. д.

Объединим всевозможные векторные произведения ортов  в таблицу: 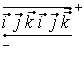.  Тогда   

                                 .

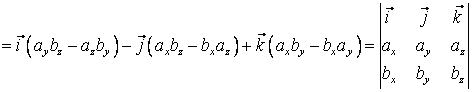Примеры   1. Найти , если ; 

2. Найти , т. А(1; -1), т.В(4; -2), т.С(3;3).

Понятие смешанного произведения векторов