Конспект лекций по дисциплине "Высшая математика", страница 33

Определение  Производной функцией  в точке х называется предел отношения приращения функции  к приращению аргумента  при условии, что последнее стремится к нулю () и этот предел существует.

Обозначается производная  или . .

Действие отыскания производной  называется дифференцированием функции .

Пример   Найти производную  функции .

По определению

.

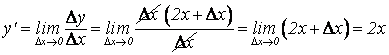Итак, . Аналогично можно показать  и т.д. Вообще, .

Физический смысл   Пусть материальная точка движется прямолинейно с переменной скоростью . Путь, пройденный точкой в момент времени t есть ; в момент времени  есть .

Величина пути за время  есть .

Средняя скорость точки за время  будет .

Мгновенная скорость точки в момент времени t будет , т.е. величина скорости в момент t есть производная от пути  по времени t.

Геометрический смысл

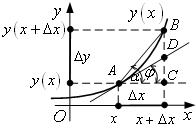АВ – хорда или секущая кривой ;

AD – касательная к  в точке х;

 – угол наклона хорды АВ к ОХ;

 – угол наклона касательной AD к ОХ;

; ;  – точка касания.

Если , то  по дуге ; хорда АВ стремится занять предельное положение касательной AD в т. х; ; . ;  .

Следовательно, , производная  от  в т. х, равна угловому коэффициенту касательной, проведенной к  в т. х.

Определение  Нормальной кривой к  в т. х называется прямая, перпендикулярная касательной.