Тогда, если ![]() изменяет свой
знак в окрестности критической точки
изменяет свой
знак в окрестности критической точки ![]() , то точка
, то точка ![]() – точка экстремума
– точка экстремума ![]() . Если
. Если ![]() изменяет
свой знак с
изменяет
свой знак с ![]() на
на ![]() ,
переходя через точку
,
переходя через точку ![]() в направлении возрастания
х, то в точке
в направлении возрастания
х, то в точке ![]()
![]() имеет
имеет
![]() , если с
, если с ![]() на
на
![]() , то в точке
, то в точке ![]()
![]() имеет
имеет ![]() .
.
Вывод
1) найти ![]() и критические точки I
рода.
и критические точки I
рода.
2) О. о. ф. поделится этими точками на интервалы монотонности.
В
каждом интервале определим знак ![]() , взяв одну
пробную точку.
, взяв одну
пробную точку.
3) Укажем точки экстремума, тип экстремума, найдем координаты этих точек на плоскости.
3. Интервалы выпуклости-вогнутости графика ![]() . Точки перегиба
. Точки перегиба
 Определение
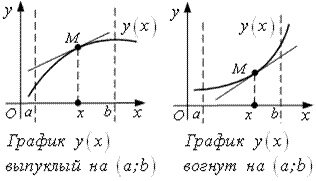
График
Определение
График ![]() называется выпуклым на интервале
называется выпуклым на интервале ![]() , если для любого
, если для любого ![]() график расположен ниже касательной к
график расположен ниже касательной к
![]() в точке х.
в точке х.
График ![]() вогнут на
вогнут на ![]() , если для любого
, если для любого ![]() график
график ![]() расположен
выше касательной к
расположен
выше касательной к ![]() в точке х.
в точке х.
 Определение
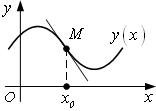
Точки графика
Определение
Точки графика ![]() , отделяющие интервалы
вогнутости от интервалов выпуклости, называются точками перегиба графика
, отделяющие интервалы
вогнутости от интервалов выпуклости, называются точками перегиба графика ![]() .
.
Точка ![]() – точка
перегиба. Касательная к
– точка
перегиба. Касательная к ![]() в точке х0
расположена с той и другой стороны кривой.
в точке х0
расположена с той и другой стороны кривой.
Необходимые и достаточные условия выпуклости-вогнутости
графика ![]()
Для того, чтобы график ![]() был
выпуклым (вогнутым) в интервале
был
выпуклым (вогнутым) в интервале ![]() , необходимо и
достаточно, чтобы для любого
, необходимо и
достаточно, чтобы для любого ![]()
![]() (
(![]() ).
).
Необходимое условие существования точки перегиба
Если точка ![]() есть точка
перегиба графика
есть точка
перегиба графика ![]() , то в этой точке
, то в этой точке ![]() или
или ![]() не
существует.
не
существует.
Такие точки , в которых ![]() обращается
в ноль или не существует, называются критическими II рода, они
принадлежат о.о.ф. и определяют интервалы выпуклости-вогнутости.
обращается
в ноль или не существует, называются критическими II рода, они
принадлежат о.о.ф. и определяют интервалы выпуклости-вогнутости.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.