Конспект лекций по дисциплине "Высшая математика", страница 15

 – уравнение называется уравнением прямой через 2 заданные точки.

Следствия:  1. Вектор  является направляющим вектором прямой.

2. Если известен направляющий вектор прямой  и точка , то ее уравнение можно записать в виде: .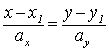

2.5. Прямая в отрезках

Ах + Ву + С = 0;  Ах + Ву = - С;  ;  ; тогда  есть уравнение прямой в отрезках; а – отрезок, отсекаемой прямой по оси ОХ; b – по оси ОУ.

2.6. Взаимное расположение прямых на плоскости

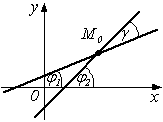1. Прямая L₁ пересекается с прямой L₂.

а) Угол γ между L₁ и L₂ можно найти по формуле:  или .

Используя понятие нормали, найдем 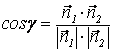, где  – нормаль L₁ ,  – нормаль L₂;

б) точку пересечения М₀(х₀,у₀) найдем, решив систему из уравнений L₁ и L₂: .

2. , следовательно,  и ; или  коллинеарна  и .

3. , следовательно,  и ; отсюда условие перпендикулярности прямых:  ;   или  и .

2.7. Расстояние от т. М₀(х₀ , у₀) до прямой L: Ах + Ву + С = 0

т.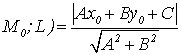, чтобы найти расстояние от т.М₀(х₀ , у₀) до прямой L: Ах + Ву + С = 0, необходимо в общее уравнение прямой, взятое по модулю, подставить координаты точки и поделить на модуль нормали  данной прямой.

2.8. Деление отрезка в данном отношении λ

Пусть задан отрезок АВ, т. А(х_А, у_А); т. В(х_В, у_В) и т.М(х, у) – делящая точка.

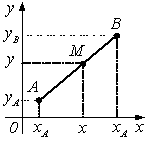Определение  т. М(х, у) делит отрезок АВ в отношении λ, если .  .

Отсюда   ; .