Конспект лекций по дисциплине "Высшая математика", страница 18

В данной системе координат т.F₁(-c;0), т.F₂(c;0). Пусть т.М(х,у) – текущая точка линии;  F₁M, F₂M – фокальные радиусы т.М.

Геометрическое свойство гиперболы:

  ;

;  ;

;

;  ;

;  ;  ;.

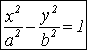  – каноническое уравнение гиперболы.

Свойства гиперболы:

1. Кривая симметрична относительно ОХ, ОУ и начала координат, т.О(0,0) – центр гиперболы.

2. Пересечение гиперболы с ОХ: ;  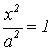;. Точки А₁(-а;0), А₂(а;0) называются действительными вершинами гиперболы, А₁А₂ - действительная ось гиперболы; А₁А₂ = 2а.

Ось ОУ гипербола не пересекает, уравнение   действительных решений не имеет. Говорят, что точки  ,  – мнимые вершины гиперболы; В₁В₂ – мнимая ось; В₁В₂ = 2b.

3. ;   и существует для любых значений у.

,    и существует при 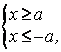   т.е. в полосе   линия не существует. Гипербола имеет две изолированные ветви с вершинами А₁(-а;0), А₂(а;0).

4. При    ветви гиперболы неограниченно приближаются к прямым, называемыми асимптотами, уравнения которых  .

5. Разворот ветвей гиперболы определяет эксцентриситет.

;     .

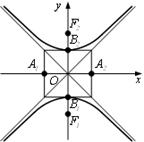Пример  Построение кривой по каноническому уравнению и отыскание параметров,  .

Если через фокусы F₁, F₂ проходит ось ОУ, а ось ОХ есть срединный перпендикуляр к отрезку F₁F₂ = 2с, то, проведя аналогичные вычисления, получим каноническое уравнение сопряженной гиперболы:    или , действительная ось которой В₁В₂, мнимая – А₁А₂.

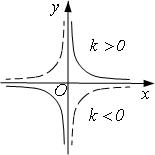
Если асимптоты гиперболы – оси координат, то гипербола называется отнесенной к осям координат, ее уравнение . Если , ветви расположены в I и III координатных углах, если , то во II и IV координатных углах. Строим кривую по точкам.