Конспект лекций по дисциплине "Высшая математика", страница 36

Дифференциал dy функции

Пример  Пусть  найдем приращение :

.

состоит из двух слагаемых; в первом слагаемом  содержится только в первой степени. Это слагаемое  называется главной линейной частью приращения . Во втором слагаемом  содержится в высшей степени, это слагаемое  называется бесконечно малой более высокого порядка, чем , обозначим его .

Определение   Дифференциалом функции  в точке х называется главная линейная часть приращения функции .

Обозначается дифференциал , т.е. в примере.

Для аргумента х , тогда имеем или . В общем случае .

Геометрический смысл дифференциала

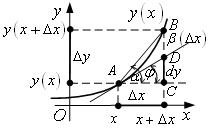АВ – хорда (секущая) кривой ;

АД – касательная к  в точке х;

 – угол наклона хорды к оси ОХ

;

 – угол наклона касательной к оси ОХ.

При     и  , т.е. ; ;  ;   или  , отсюда , т.е. ; ; .

Следовательно, дифференциал  функции  в точке х равен приращению ординаты точки касательной, проведенной к  в точке х, если х получает приращение .

Свойства