Годовая эффективная ставка r – это годичная ставка сложного процента,
которая дает тот же финансовый результат, что и m-кратное наращение в
год по ставке 
%.
Другими словами, ежегодное начисление процентов по годовой эффективной ставке r
в течение T лет обеспечивает такое же соотношение между вложенной и
полученной суммами 
,
что и при начислении процентов за m периодов продолжительностью t
дней исходя из годовой расчетной ставки i% также в течение T лет. Она вычисляется по стандартной формуле:
,
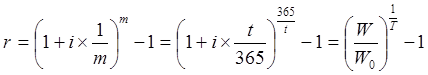где r – годовая эффективная ставка процента (в долях единицы); i – годовая расчетная ставка процента (в долях единицы); m – число периодов начисления процентов в году; t – договорный срок вклада в днях; W0 – исходная сумма капитала; .W – конечная сумма капитала; T – общий срок хранения средств на данном виде вклада в годах.
Для условий данного вклада годовая эффективная ставка будет рассчитана как
.
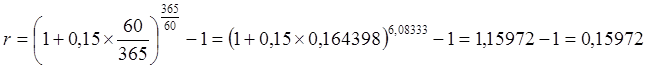Таким образом, годовая эффективная ставка для срочного вклада сроком 60 дней при расчетной ставке 15% годовых составит 15,97% годовых, то есть каждый рубль, помещенный на депозит, принесет за год 15,97 копеек. Точно такой же доход был бы получен при помещении средств на годовой срочный вклад под 15,97% годовых.
Примечание. Если бы мы просто рассчитали доходность данного вклада за один год хранения, то нам пришлось бы учесть, что вклад пролежит шесть полных сроков и еще 4 дня, за которые должна быть начислена ставка по вкладам до востребования.
Доходность годовой финансовой операции y рассчитывается как отношение прироста капитала (W–W0) за год к величине первоначально вложенного капитала W0. Вычисленный показатель доходности в этом случае будет ниже, чем годовая эффективная ставка, и составляет 15,93%.
.
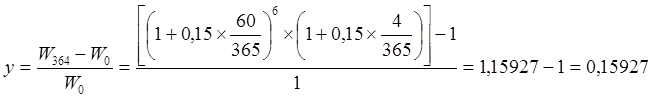Задача 7
Студент в день своего 20-летия открыл срочный вклад на 1 месяц на сумму 500 рублей на условиях неоднократного автоматического переоформления срочного договора. По этому вкладу начисляется 5% годовых. С тех пор в последний день очередного срока студент вносит дополнительный взнос в размере 500 рублей.
а) В каком возрасте он станет миллионером ( в предположении, что процентная ставка будет неизменной)?
б) По какой ставке должен начисляться процентный доход, для того чтобы удалось скопить требуемую сумму к 50-летию?
В данной задаче неизвестна точная дата открытия вклада. Поэтому ответ можно найти лишь приближенный, но с высокой степенью точности, так как придется предположить, что все месяцы имеют равную продолжительность, и не учитывать фактор високосных лет.
а) Пусть t – искомый срок в месяцах. В начале первого месяца студент вносит на счет W0 = 500 рублей. На конец первого месяца сумма вклада W1 составит
руб.
К этой сумме будет добавлено 500 руб., так что базой начисления процентов будет 1002,083 руб. На конец второго месяца вклад возрастет до
руб.
На конец третьего месяца вклад будет равен:
руб.
И так далее в течение t месяцев. Таким образом, на первые внесенные 500 рублей начисление и капитализация процентов будут произведены t раз, на вторую сумму 500 рублей – (t-1) раз, на третью сумму – (t-2) раз, и на последние пятьсот рублей – один раз. В общем случае процесс увеличения вклада описывается рядом, состоящим из t платежей с начисленными процентами. Сумма этого ряда Wt и составит конечную величину вклада, то есть:
.
Вынесем общий множитель за скобки.
.
В квадратных скобках оказалась сумма
геометрической прогрессии с числом членов t, первый член которой равен 1, а знаменатель q=
.
Сумма геометрической
прогрессии вычисляется по известной формуле:
.
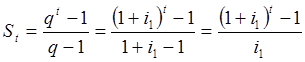Таким образом, конечная величина вклада равна
.
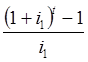Составим уравнение, решив которое относительноt, можно будет узнать, когда состояние студента достигнет 1 млн. руб. Для этого проведем преобразования и прологарифмируем обе части уравнения:
;
;
;
;
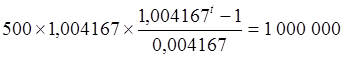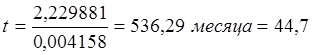года.
Таким образом, студент станет миллионером в возрасте 64 года 8 месяцев и 9 дней.
Примечание. В ходе решения мы записали выражение
.
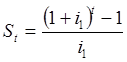Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.