Депозитные операции. Диверсификация вкладов. Валютные операции. Кредитные операции. Операции с ценными бумагами, страница 17

Обозначим банкротство i–го банка как событие Б_i. Вероятность условия – это вероятность банкротства правительства P{Б_прав} = 0,08. Противоположным данному событию является сохранение финансовой стабильности правительства, вероятность которого равна 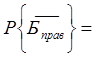 1–P{Б_прав} = 1–0,08 = 0,92. Если банкротства правительства не происходит, то условные вероятности разорения банков равны

P{Б₁|} = 0,05; P{Б₂|} = 0,08; P{Б₃|} = 0,11.

Если же банкротство правительства совершилось, то условные вероятности банкротства банков равны

P{Б₁|Б_прав} = 0,1; P{Б₂|Б_прав} = 0,16; P{Б₁|Б_прав} = 0,22.

Для того чтобы вычислить безусловную вероятность события, следует учесть вероятность самого условия. Поэтому безусловная вероятность определяется как произведение условной вероятности и вероятности условия. Отсюда безусловная вероятность банкротства банка  или полная вероятность банкротства) при любом исходе для правительства определяется как сумма вероятностей двух событий. Первое событие состоит в том, что за банкротством правительства последует банкротство i–го банка, а второе означает что i–ый банк разорится даже при условии сохранения правительства.

Полная вероятность разорения первого банка вычисляется:

P{Б₁}= P{Б₁|Б_прав}× P{Б_прав}+ P{Б₁|}× P{}= 0,1×0,08+0,05×0,92 =

= 0,054 = 5,4%

Для второго банка:

P{Б₂}= P{Б₂|Б_прав}× P{Б_прав}+ P{Б₂|}× P{}= 0,16×0,08+0,08×0,92 =

= 0,0864 = 8,64%

Для третьего банка:

P{Б₃}= P{Б₃|Б_прав}× P{Б_прав}+ P{Б3|}× P{}= 0,22×0,08+0,11×0,92 =

=0,1188 = 11,88%

Задача 3

В городе четыре банка. Годовая эффективная ставка процента по срочным вкладам на год во всех банках составляет 20%. Вероятность банкротства любого банка в течение ближайшего года составляет 10%. Банкротство банка означает потерю всех вложенных в него денег. Вкладчик распределяет свои средства (1000 рублей.) поровну между выбранными банками. Определите математическое ожидание получаемой через год суммы, вероятности получить максимум, получить часть и потерять все в случае, если: а) все средства вложены в один банк; б) в два банка; в) в три банка; г) в четыре  банка. Задачу решить в предположении, что банкротство любого банка повышает вероятность банкротства остальных в 2 раза.

Вероятность банкротства любого из банков P{Б_i} = 0,1. Соответственно, вероятность выживания банка, как противоположного события равна P{}=(1‑0,1) = 0,9. Но при условии реализации этого события, то есть при P{Б_i} = 1 вероятность банкротства любого из оставшихся банков возрастает до 20%. P{Б_j|Б_i} = 0,2.

В кодированном виде возможные события образуют набор из 16 событий от {0000} до {1111}, где «0» ‑ банкротство, «1» ‑ сохранение любого из банков. Рассчитаем вероятности всех возможных событий.

1.  Благополучие всех банков – событие {1111}.

P{1111}= 0,9⁴ = 0,6561.

Следовательно, суммарная вероятность всех остальных исходов, включающих банкротство хотя бы одного банка, является противоположным событием.

P{0000}+P{0001} + … +P{0111} = 1–P{1111}= 1–0,6561 =0,3439.

С вероятностью 34,39% может разориться любой набор банков от одного до четырех банков в любой последовательности. Вычислим вероятность того, что первым в цепочке банкротств окажется конкретный банк – 1-ый, 2-ой, 3-ий или 4-ый. Эти возможности равновероятны. Поэтому P{Б_n}=, где {Б_n} – событие, состоящее в том, что крах банковской системы начался с банкротства n–го банка.

Зная вероятность условия P{Б_n}, можно рассчитать далее безусловные вероятности всех возможных событий P{Б_m×Б_n}.

P{Б_m× Б_n}= P{Б_m|Б_n}× P{Б_n} – это вероятность того, что за банкротством n-го банка последует банкротство m–го банка.

2.  Банкротство всех банков после краха одного из них – событие {0000}.