Мы получили три разных значения последнего платежа P5. В использованных методах расчета стоимости кредита формула простых процентов дает различные результаты в зависимости от того, к какому моменту времени приводились денежные суммы: а) к началу каждого месяца; б) к концу общего срока кредитования или в) к началу периода кредитования.
Следует отметить, что приведение денежных сумм к концу периода (метод торговца) дает более низкую стоимость кредита, чем приведение к началу периода (метод дисконтирования). Актуарный метод дает самый высокий результат, так как возникает начисление процентов на проценты.
задача 7
Если в условиях задачи 5 будет применяться формула сложных процентов (годовая эффективная ставка 24%) будут ли получены разные величины номинальной стоимости кредита при расчете по актуарному методу, методу торговца и методу дисконтирования?
Для ответа на вопрос воспользуемся решением задачи 6, заменив значения простых ставок процента за период сложными. Если годовая эффективная ставка r равна 24%, то соответствующая ей месячная ставка равна
.
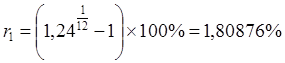Вычислим значения P5 по каждому из трех рассмотренных методов:
а) Актуарный метод.
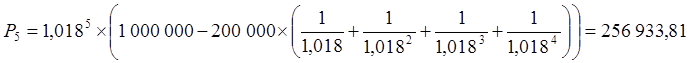руб.
б) Метод торговца.
руб.
В) Метод дисконтирования.
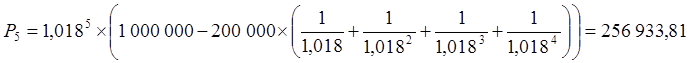руб.
Следовательно, применение формулы сложных процентов дает одинаковый результат независимо от используемого метода расчета стоимости кредита. Действительно, при подстановке ставок сложного процента за соответствующие периоды все три формулы оказываются математически идентичными.
Следует отметить, что различия при расчетах по формуле простых и сложных процентов возникают при сроках кредита менее одного года. Если срок кредита более года и измеряется целым числом лет, то формулы простых и сложных процентов дают идентичные результаты.
задача 8
Кредиты на 5 месяцев выдаются исходя из расчетной ставки 25% годовых.
Исходя из какой расчетной ставки должны выдаваться кредиты на 1 месяц, чтобы годовая эффективная ставка процента по таким кредитам была такой же, как и по кредитам на 5 месяцев?
Если две расчетные годовые процентные ставки 
и
(с
числом капитализаций процента в году 
и
,
соответственно) при одном и том же начальном капитале обеспечивают одинаковый
процент за равные промежутки времени, то речь идет об эквивалентных номинальных
годовых процентных ставках.
Запишем условие эквивалентности номинальных годовых процентных ставок:
.
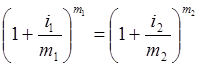Если кредит выдается на t1=5 месяцев, то число капитализаций m1 равно 12/t1=12/5 или 2,4 раза в год.
При сроке кредита t2=1 месяц число капитализаций m2 достигает 12 раз в год.
Неизвестную ставку i2 найдем из условия эквивалентности ставок:
.
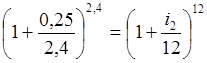Таким образом, имеем:
.
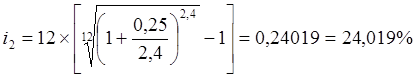Проверим найденный ответ:
;
.
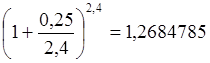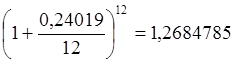Как видно, и расчетная годовая ставка 25% по 5-месячным кредитам, и расчетная годовая ставка 24,019% по 1-месячным кредитам обеспечивают кредитору годовой доход в размере 26,8 копеек на 1 рубль ссужаемых средств, то есть годовая эффективная ставка по обоим видам кредитов составляет 26, 8%.
Задача 9
Гражданин Петров купил мебель в рассрочку. Для этого в магазине ему пришлось оформить кредит на сумму 20 тысяч рублей сроком на 6 месяцев из расчета 36% годовых. Кредит был выдан 14 октября 2003 г. По условиям кредита возврат основной части долга предусматривался в конце каждого месяца равными суммами с одновременной выплатой процентов на остаток долга. Необходимо:
а) Составить расписание погашения кредита и рассчитать его номинальную стоимость;
б) рассчитать эффективную ставку кредита
а) За первый месяц пользования кредитом, с 14-го октября по 13 ноября, будут начислены проценты за 31 день. Ставка процента за 1-ый месяц составит
.
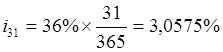Кредит будет погашаться шестью равными долями:
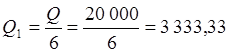руб.
В конце первого месяца клиент должен заплатить за пользование всей суммой кредита в течение 31 дня. Начисленные проценты составят
руб.
Всего следует выплатить в конце первого месяца
P1=3 333,33+611,51=3 944,84 руб.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.