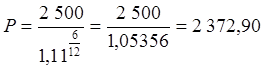Депозитные операции. Диверсификация вкладов. Валютные операции. Кредитные операции. Операции с ценными бумагами, страница 35

 руб.

Для того чтобы оценить рыночную стоимость облигации за год до погашения, следует дисконтировать ее номинальную стоимость по годовой ставке процента:

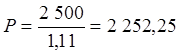 руб.

По результатам решения задач 1 и 2 можно построить график изменения рыночной цены дисконтной облигации в течение срока ее жизни: от момента выпуска до погашения.

P

                                                                         2435,62      2500

2252,25

2029,06

t

Задача 3

Номинал дисконтной облигации составляет 2 500  рублей. В настоящий момент на фондовом рынке эти облигации продаются по 2 200 рублей. Годовая эффективная ставка процента на денежном рынке – 11%. Дата погашения облигации – 15 декабря 2004 года. Сколько дней осталось до погашения облигации? С какого дня рыночная цена облигации превысит 2 450 рублей?

Покупая сегодня такую облигацию, инвестор совершает операцию, эквивалентную выдаче кредита в размере 2 200 рублей на срок T, по истечении которого ему вернут сумму 2 500 рублей. В эту сумму войдут 2 200 рублей основного кредита и проценты, начисленные по годовой ставке сложного процента 11% за срок T.

N=2500

 

                                                           T=?

P=2200

Схема операции показана на графике. Отсюда можно записать уравнение, связывающее настоящую и будущую стоимости облигации:

, или .

Решая уравнение относительно T, находим, сколько дней осталось до даты погашения облигации:

;

;

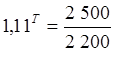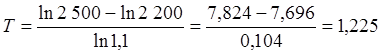 года.

Следовательно, облигация будет погашена по номиналу через  дней. Следовательно, сегодня – 24 сентября 2003 г., то есть 15 декабря 2004 г. минус 447 дней.

Аналогично определяем дату, начиная с которой цена облигации превысит 2 450 рублей. Сначала вычисляем, сколько дней останется от этой даты до даты погашения:

;

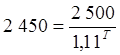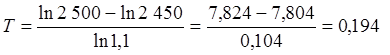года = 70,7 дней.

Следовательно, цена облигации превысит 2 450 рублей, начиная с 5 октября 2004 г. (15 декабря 2004 г. минус 70 дней).

Задача 4

Дисконтная облигация номинальной стоимостью 2 500 рублей приобретена за полтора года до погашения по курсу 90. Рассчитайте доходность облигации к погашению.

Показатель доходности за период владения ценной бумагой выявляет, насколько эффективной была операция покупки-продажи ценной бумаги, какой эффект дала инвестиция в данную бумагу. В самом общем случае он вычисляется как отношение прироста дохода к величине вложенного капитала за период владения ценной бумагой.

Если ценная бумага, приобретенная по цене P₀, обеспечивает регулярные выплаты A, и ее рыночная цена  за период t возрастает до P_t, то полная доходность y за период владения может быть вычислена следующим образом:

.

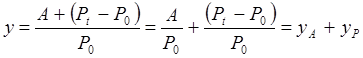Здесь A – поток текущих доходов, P₀ – первоначальная сумма вложенного капитала (инвестиции на начало периода, покупная стоимость ценной бумаги), P_t – конечная сумма вложенного капитала (инвестиции на конец периода, продажная стоимость ценной бумаги), y_A – текущая доходность, y_P – доходность прироста капитала (капитализированная доходность), y – полная доходность.

Для того чтобы учесть возможность реинвестирования доходов в течение периода владения облигацией, применяют показатель доходности к погашению. Доходность к погашению представляет собой эффективную процентную ставку (в годовом исчислении), дисконтирование по которой приравнивает величину совокупных доходов к сумме первоначальных инвестиций. Она определяется из уравнения, в котором текущая стоимость облигации определяется как сумма текущих выплат и номинала, выплачиваемого при погашении, приведенных к начальному моменту времени с использованием показателя доходности к погашению.

.

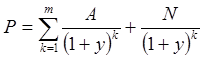Полная доходность дисконтной облигации или облигации с нулевым купоном включает в себя только вторую составляющую – прирост стоимости капитала y_P. Доход возникает только за счет изменения фактической рыночной (курсовой) стоимости облигации, так как купонные выплаты отсутствуют. Курс облигации вычисляется как отношение ее фактической  рыночной стоимости к номиналу, выраженное в процентах.