Депозитные операции. Диверсификация вкладов. Валютные операции. Кредитные операции. Операции с ценными бумагами, страница 25

а) кредиты на такие сроки предоставляются исходя из расчетной ставки 14% годовых, а для исчисления стоимости кредита используется формула простых процентов;

б) для кредитов на любые сроки используется годовая эффективная ставка – 14%?

а) Временнáя диаграмма, построенная для условий данной задачи, показывает, что кредит будет выдан на оговоренную сумму за вычетом процентов (650 000 – I) , а основной долг  (650 000 руб.) будет возвращен спустя 4,5 месяца.

Q=650000 руб.

4,5                                            t (мес.)

I=?                                                                                         

P=650000 руб.=Q

Запишем условие эквивалентности во времени выданной и возвращаемой денежных сумм:

.

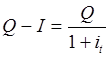В этом уравнении все платежи и поступления денежных средств рассматриваются на один момент времени – момент выдачи ссуды. Поэтому выданная ссуда и уплаченные проценты входят в уравнение с коэффициентом 1, а возврат основной части долга – с множителем дисконтирования , в котором i_t– ставка за период (4,5 месяца). Таким образом, умножая будущий платеж на множитель дисконтирования, мы «приводим» его к настоящему моменту времени. Отсюда следует, что

;

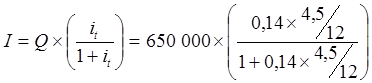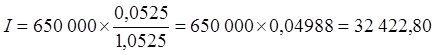 руб.

Примечание. Это – пример антисипативного начисления процентов, когда плата за кредит устанавливается, как скидка с выдаваемой в долг суммы Ставка антисипативного процента называется также учетной ставкой и широко применяется в операциях с векселями. Ставка антисипативного процента здесь равна 4,988% за 4,5 месяца. Сумма выплачиваемых процентов в этом случае оказывается меньше, чем в случае возврата кредита и процентов в конце срока, который был описан в условии задачи 2, потому что заемщик выплачивает проценты раньше – в момент выдачи кредита.

До сих пор во всех задачах применялось декурсивное начисление процента. При декурсивном начислении процента ставка устанавливается по отношению к выданной сумме (в начале периода), а при антисипативном начислении – по отношению к возвращаемой сумме. В данном случае плата за кредит (32 422,8 руб.) составляет 5,25% от выданной суммы (650 000-32 422,8=617 577,2 руб.) и 4,988% от возвращаемой суммы (650 000 руб.).

б) При начислении сложных процентов декурсивная ставка сложного процента за срок 4,5 месяца составит 5,036%, поэтому стоимость кредита будет меньше.

.

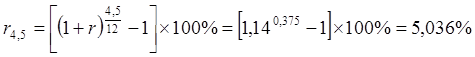Уравнение, записанное для случая (а), модифицируется следующим образом:

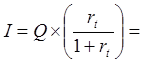
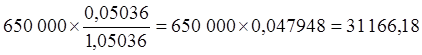 руб.

Антисипативная ставка сложного процента за срок 4.5 месяца в данном случае равна 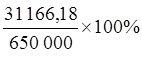=4,795%.

Задача 5

Заем на 1 миллион. рублей взят на 5 месяцев при условии возврата основного долга ежемесячно равными частями и единовременной уплаты процентов по истечении пяти месяцев. Используется формула простых процентов (ставка 24% годовых). Какой будет номинальная стоимость кредита, если расчет стоимости кредита осуществляется:

а) по актуарному методу;

б) по методу торговца;

в) по методу дисконтирования?

В данных условиях заемщик должен погашать по одной пятой кредита, то есть по 200 000 руб. в конце каждого месяца. Но последний, пятый платеж будет включать в себя не только последнюю часть возвращаемого кредита (200 000 руб.), но и все накопленные по ссуде и не погашенные проценты. Необходимо рассчитать величину последнего платежа.

А) В общем случае схема актуарного метода выглядит следующим образом.

В течение первого периода за должником числится вся сумма долга, и на нее начисляются проценты, что увеличивает общую задолженность. В конце первого периода должник возвращает первую часть ссуды. Это уменьшает его задолженность. Тогда в течение второго периода проценты начисляются на остаток ссуды плюс на уже начисленные, но не выплаченные проценты. И так далее, пока не наступит срок окончательного платежа, когда будет возвращена последняя часть плюс все накопленные проценты. Если очередной платеж меньше накопленных и непогашенных процентов, то уменьшение суммы долга не производится, а сумма платежа присоединяется к следующему платежу.